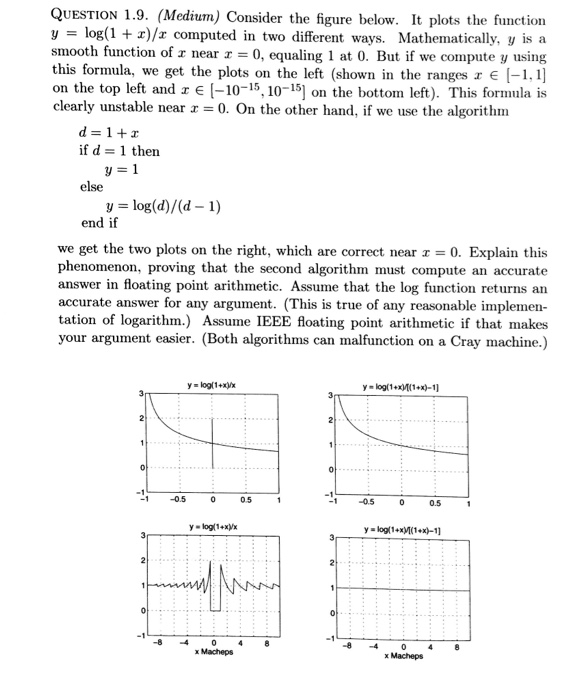
Consider the figure below. It plots the function y = log(1 + x)/x computed in two different ways. Mathematically, y is a smooth function of x near x = 0, equaling 1 at 0. But if we compute y using this formula, we get the plots on the left (shown in the ranges x belongsto [-1, 1] on the top left and x belongsto [-10^-15, 10^-15] on the bottom left). This formula is clearly unstable near x = 0. On the other hand, if we use the algorithm d = 1 + x if d = 1 then y = 1 else y = log (d)/(d - 1) end if we get the two plots on the right, which are correct near x = 0. Explain this phenomenon, proving that the second algorithm must compute an accurate answer in floating point arithmetic. Assume that the log function returns an accurate answer for any argument. (This is true of any reasonable implementation of logarithm.) Assume IEEE floating point arithmetic if that makes your argument easier. (Both algorithms can malfunction on a Cray machine.)