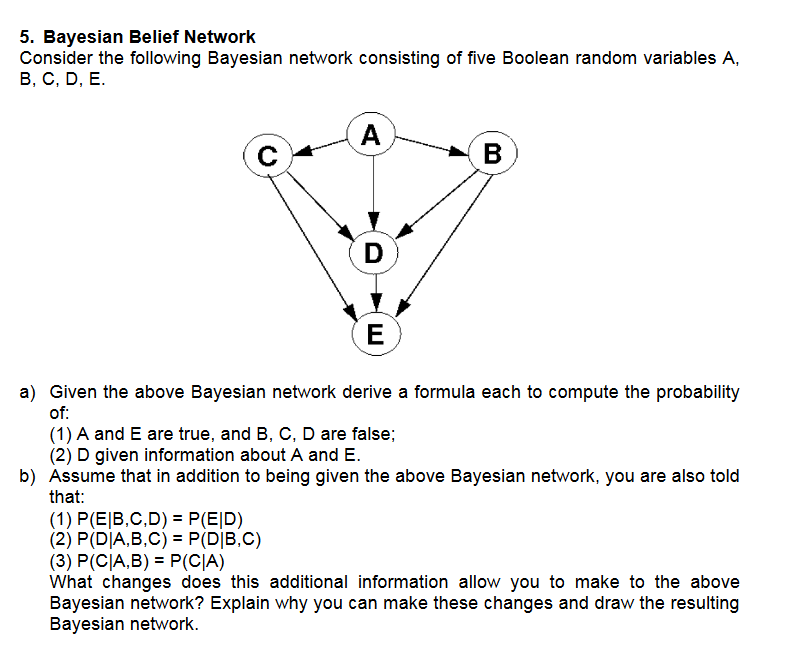
Consider the following Bayesian network consisting of five Boolean random variables A, B, C, D, E. a) Given the above Bayesian network derive a formula each to compute the probability of: (1) A and E are true, and B, C, D are false; D given information about A and E. b) Assume that in addition to being given the above Bayesian network, you are also told that: P(E|B, C, D) = P(E|D) P(D|A, B, C) = P(D|B, C) P(C|A, B) = P(C|A) What changes does this additional information allow you to make to the above Bayesian network? Explain why you can make these changes and draw the resulting Bayesian network. Consider the following Bayesian network consisting of five Boolean random variables A, B, C, D, E. a) Given the above Bayesian network derive a formula each to compute the probability of: (1) A and E are true, and B, C, D are false; D given information about A and E. b) Assume that in addition to being given the above Bayesian network, you are also told that: P(E|B, C, D) = P(E|D) P(D|A, B, C) = P(D|B, C) P(C|A, B) = P(C|A) What changes does this additional information allow you to make to the above Bayesian network? Explain why you can make these changes and draw the resulting Bayesian network