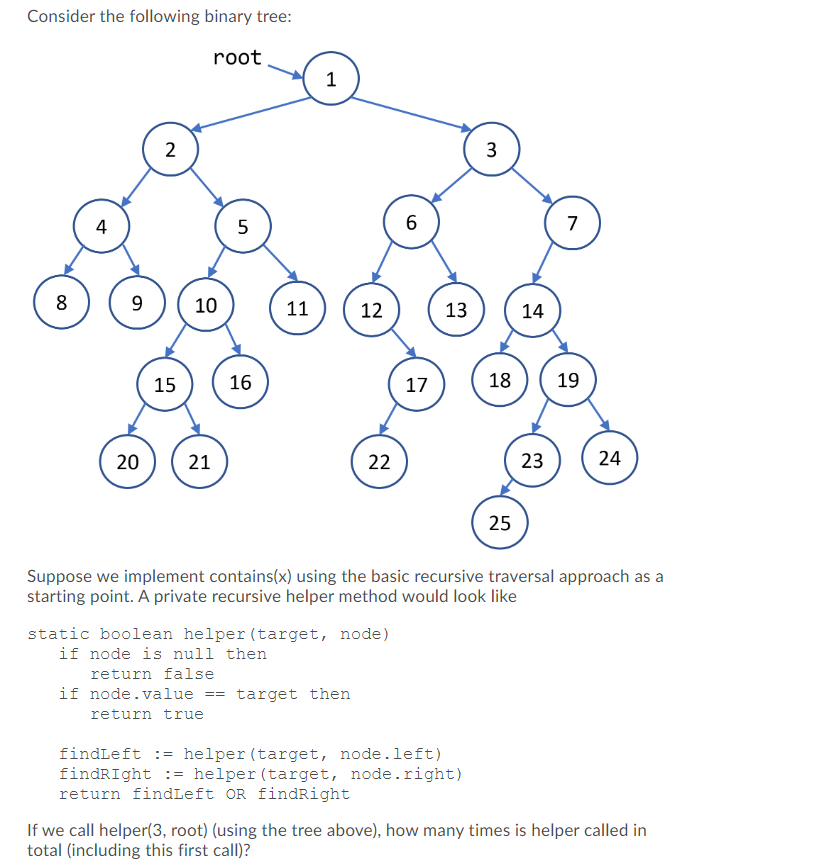
Consider the following binary tree: root 8 00 2 1 6 4 5 6 20 20 15 3 10 11 12 13 14 21 24 16 7 17 18 19 22 22 23 24 25 Suppose we implement contains(x) using the basic recursive traversal approach as a starting point. A private recursive helper method would look like static boolean helper (target, node) if node is null then return false if node.value == target then return true findLeft := helper (target, node.left) findRIght := helper (target, node.right) return findLeft OR findRight If we call helper(3, root) (using the tree above), how many times is helper called in total (including this first call)?