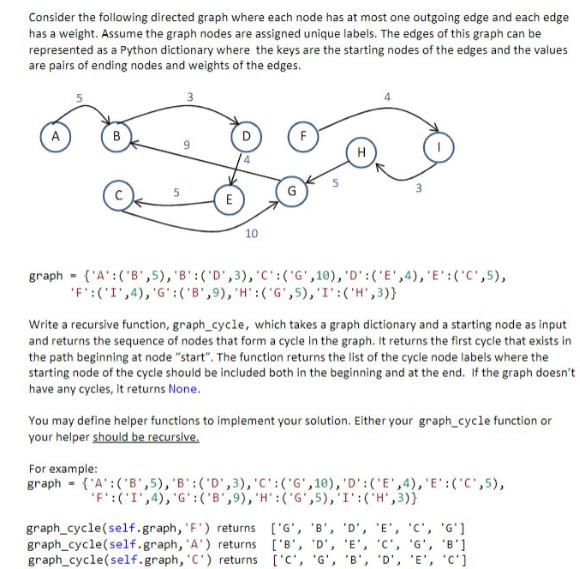
Consider the following directed graph where each node has at most one outgoing edge and each edge has a weight. Assume the graph nodes are assigned unique labels. The edges of this graph can be represented as a Python dictionary where the keys are the starting nodes of the edges and the values are pairs of ending nodes and weights of the edges. 5 - 3 E 10 H graph ('A': ('B',5), 'B': ('D', 3), 'C': ('G',10), 'D': ('E',4), 'E': ('C',5), 'F': ('I',4), 'G': ('B',9), H:('G',5), 'I': ('H',3)} Write a recursive function, graph_cycle, which takes a graph dictionary and a starting node as input and returns the sequence of nodes that form a cycle in the graph. It returns the first cycle that exists in the path beginning at node "start". The function returns the list of the cycle node labels where the starting node of the cycle should be included both in the beginning and at the end. If the graph doesn't have any cycles, it returns None. You may define helper functions to implement your solution. Either your graph_cycle function or your helper should be recursive. For example: graph ('A': (8,5), 'B:('D',3), 'C':('G',10), 'D':('E',4), 'E': ('C',5), 'F':('I',4), 'G': ('B',9), 'H': ('G',5), 'I':('H',3)} graph_cycle(self.graph, 'F') returns ['G', 'B', 'D', 'E', 'C', 'G'] graph_cycle(self.graph, 'A') returns ['B', 'D', 'E', 'C', 'G', 'B'] graph_cycle(self.graph, 'C') returns ['C', 'G', 'B', 'D', 'E', 'C']