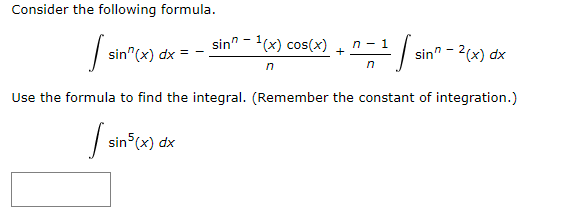
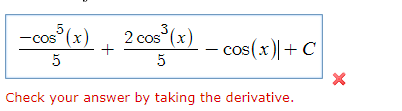
Consider the following formula. sin"(x) dy = _ sin" (x) cos(x) n- 1 + sin? - 2(x) dx n Use the formula to find the integral. (Remember the constant of integration.) sin (x) dx\f1 ) [ sin ( x ) . dx here, n= 5 5 - 1 : sinuajax = - sin ( x ). Cosix ) 5 - 1 5 - 2 + 5 sin ( 2 ) do 5 1 - sin (x ) cos (2) + 5 Sin la ). dx 5 3 - 2 - sin (x). cos ( x ) - sin (x ) . cost 3 . Sin ( x ). dx + vilI + 3 5 3 - sin (x). cosix) - sinih ) . costa ) + 2 x 1 6 sinlay da + 5 3 4 , - Sin '(2). Cos(x ) - 4 sing() . cosla ) thx2 ( - cosx ) + C 5 15 - Sin (*). cos (x) _ 4 sin?(x). cos( ) -& cosla)+ ( 5 15 sin ( x ) dx = - sin (x) cos(x ) - 4 sin2(x). cos (x) _8 cos(x ) + C 5 15 15