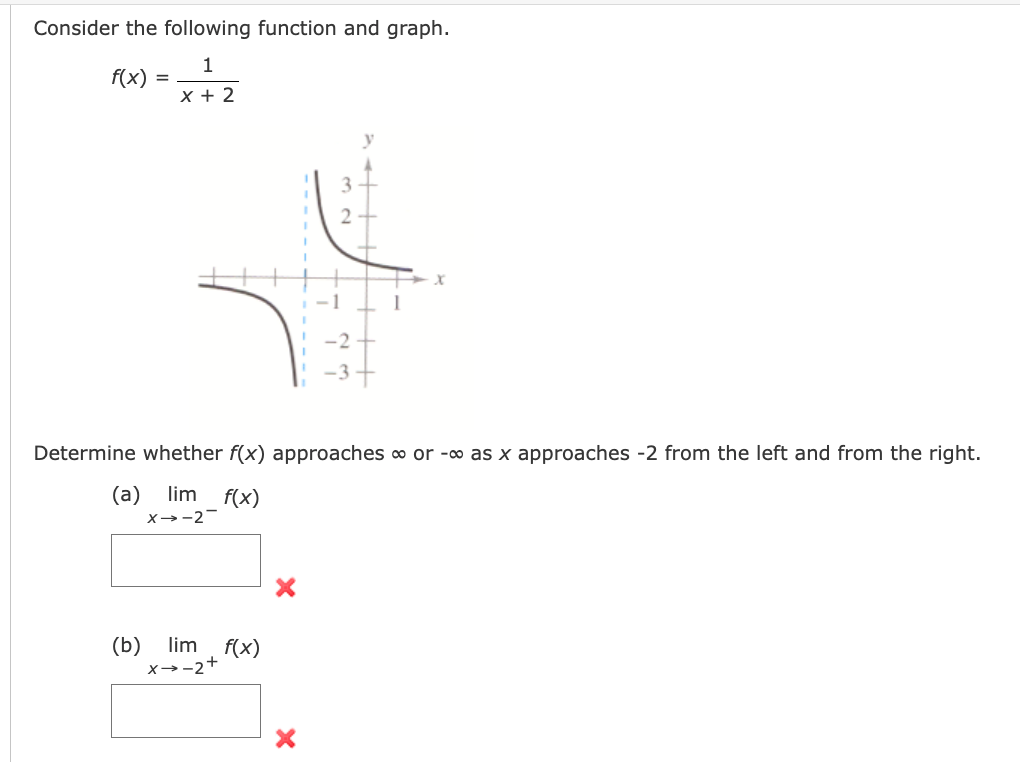
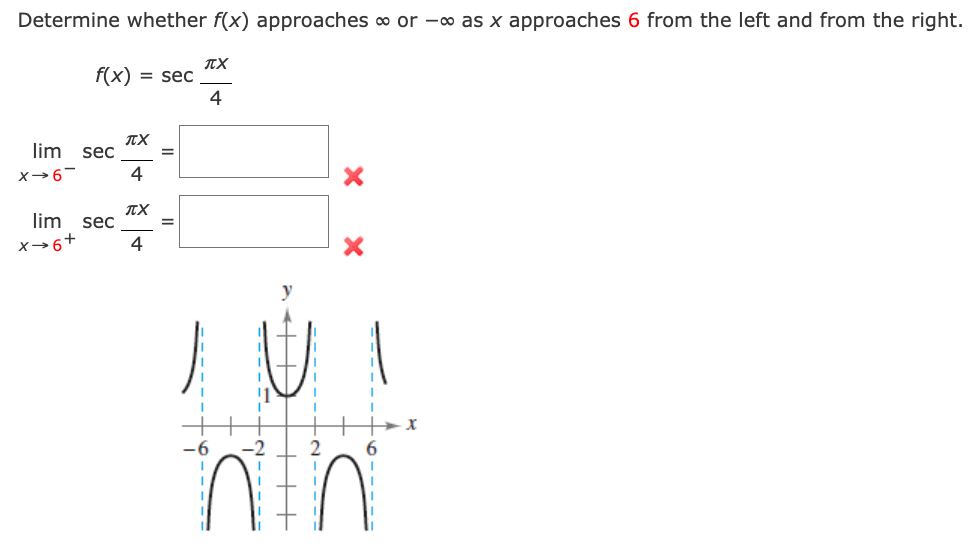
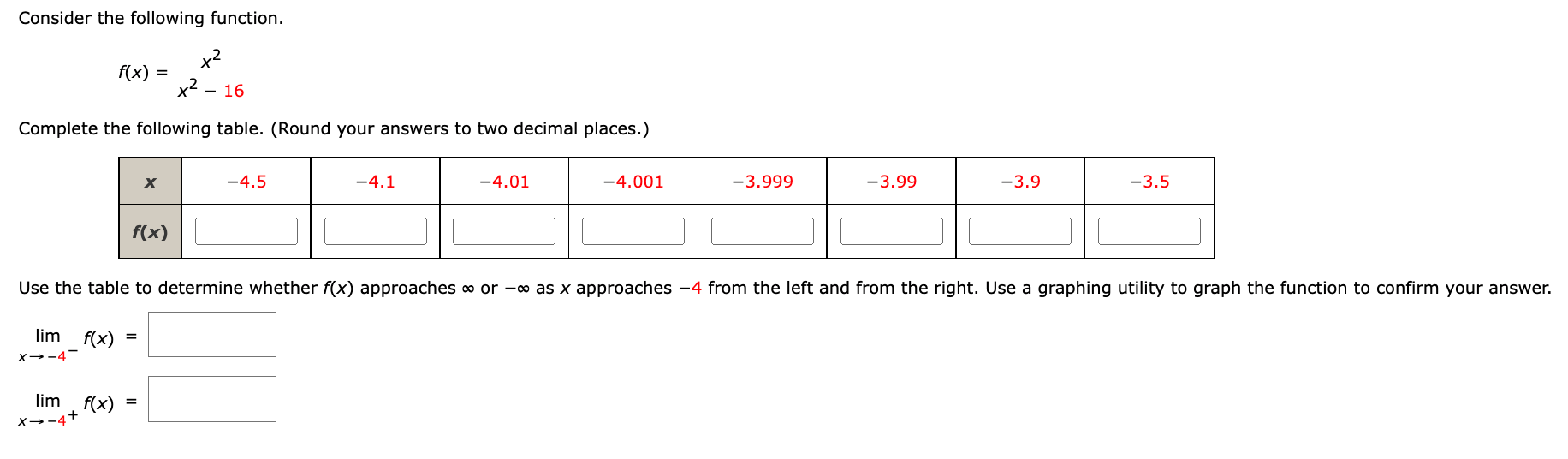
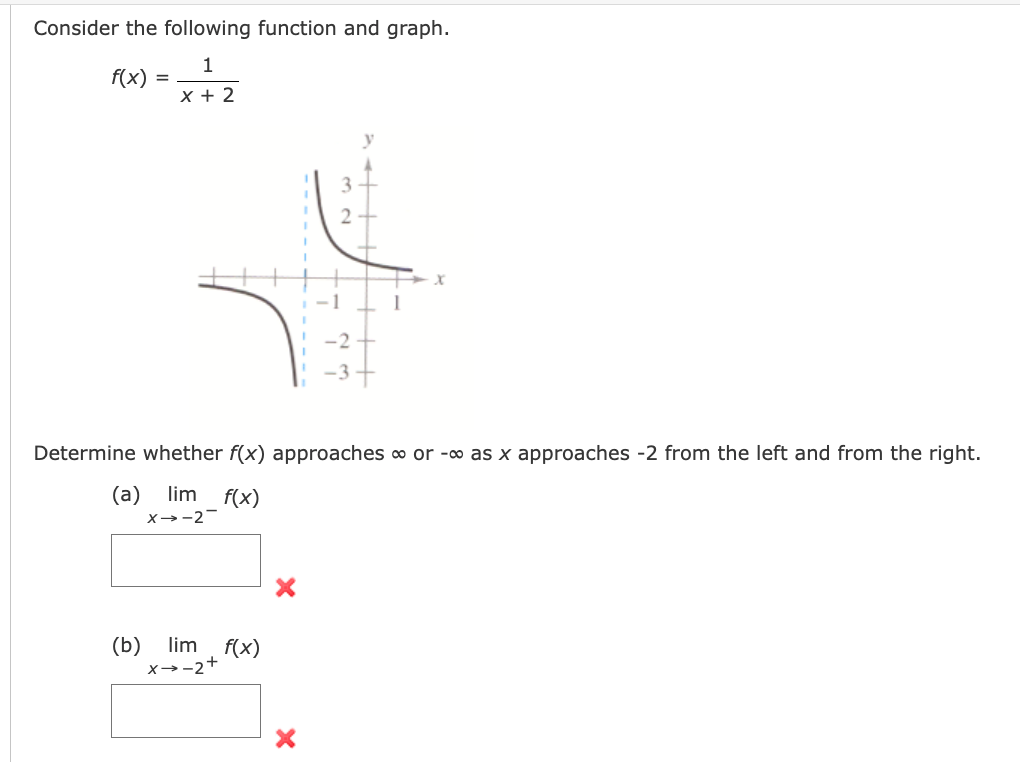
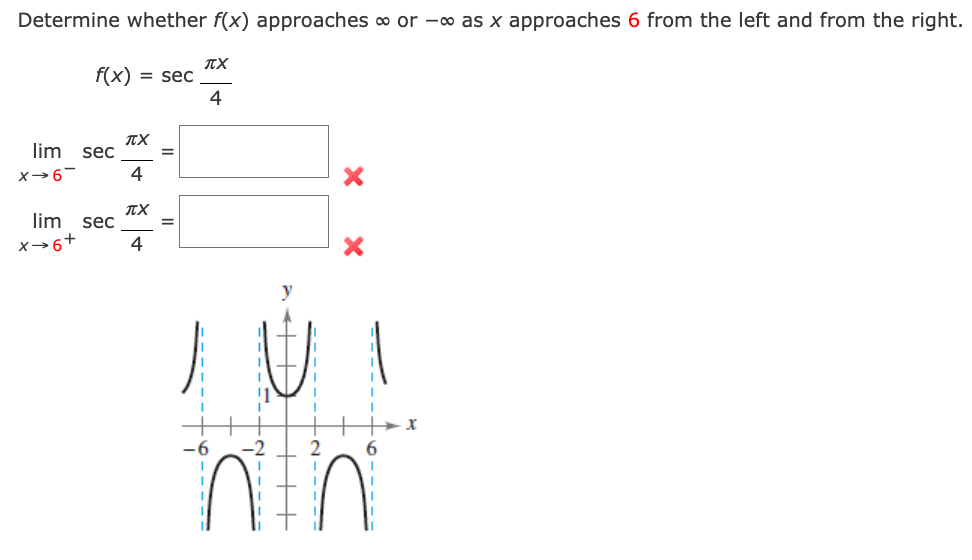
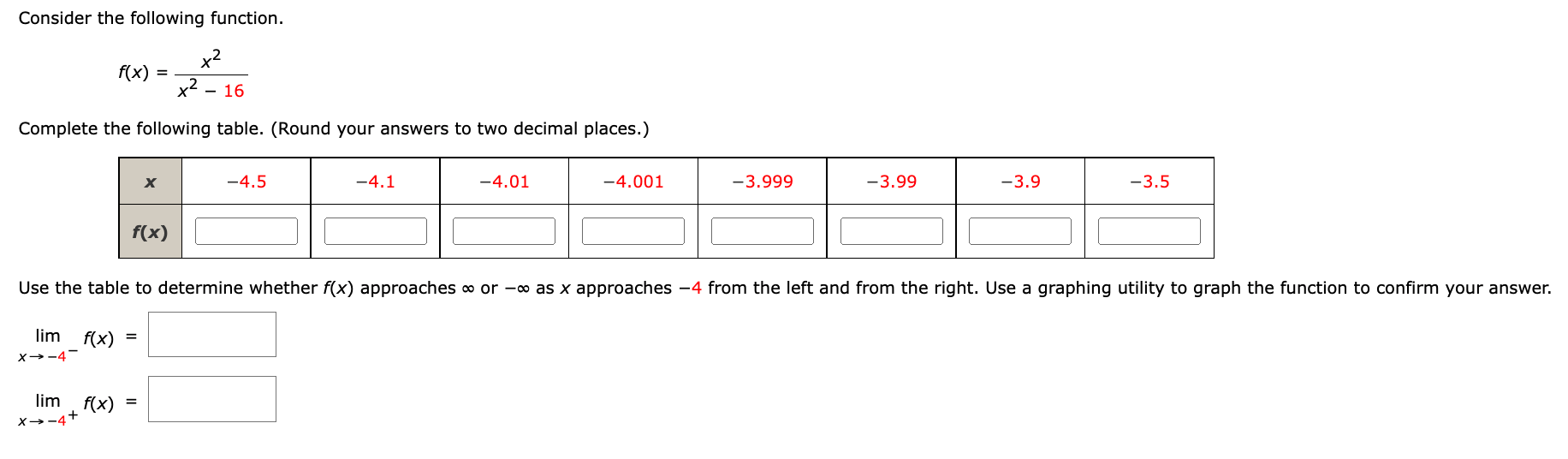
Consider the following function and graph. f ( x ) = _ 1 x+ 2 3 - - - - 2 -1 Determine whether f(x) approaches co or -co as x approaches -2 from the left and from the right. (a) lim f(x) x - -2 X (b) lim f(x) x - - 2+ XDetermine whether f(x) approaches co or -co as x approaches 6 from the left and from the right. JX f(x) = sec 4 lim sec X- 6 4 X lim sec x- 6+ 4 X Thre - - - - X inthiConsider the following function. 1 m =W Determine whether f(x) approaches on or oo as x approaches 2 from the left and from the right. (3) lim x) X42 Consider the following function. f (x) = x2 X2 - 16 Complete the following table. (Round your answers to two decimal places.) X -4.5 -4.1 -4.01 -4.001 -3.999 -3.99 -3.9 -3.5 f(x) Use the table to determine whether f(x) approaches co or - as x approaches -4 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. lim f(x) = X- -4 lim f(x) = x - - 4+Find the vertical asymptotes (if any) of the graph of the function. (Enter your answers as a comma-separated list of equations. If an answer does not exist, enter DNE.) X2 X)=7 x225 Ex