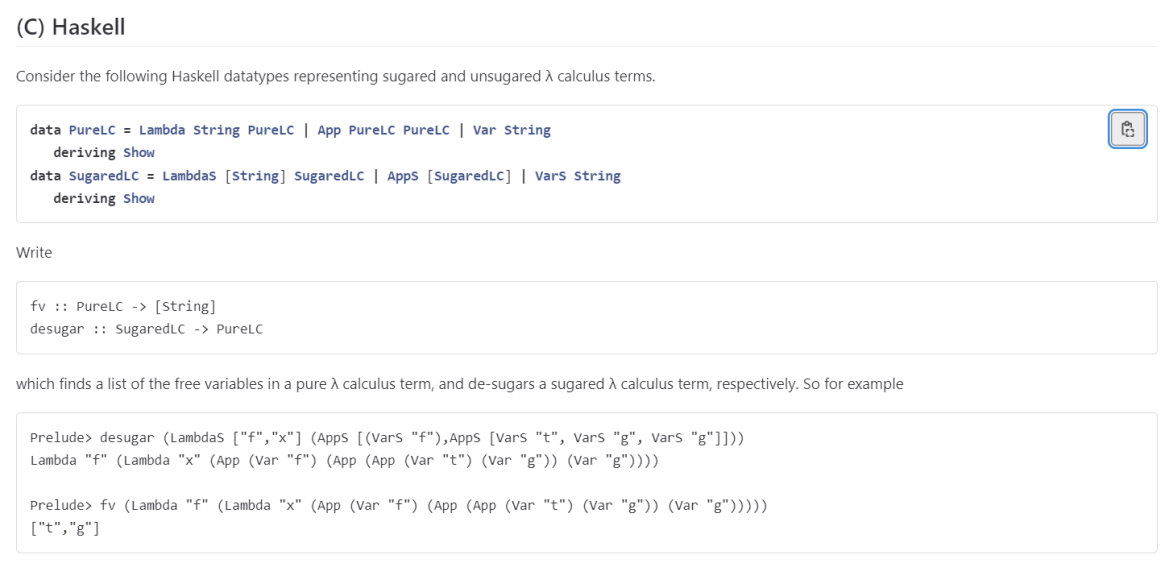
Consider the following Haskell datatypes representing sugared and unsugared calculus terms.

data PureLC = Lambda String PureLC | App PureLC PureLC | Var String deriving Show data SugaredLC = LambdaS [String] SugaredLC | AppS [SugaredLC] | VarS String deriving Show

Write

fv :: PureLC -> [String] desugar :: SugaredLC -> PureLC

which finds a list of the free variables in a pure calculus term, and de-sugars a sugared calculus term, respectively. So for example

Prelude> desugar (LambdaS ["f","x"] (AppS [(VarS "f"),AppS [VarS "t", VarS "g", VarS "g"]])) Lambda "f" (Lambda "x" (App (Var "f") (App (App (Var "t") (Var "g")) (Var "g")))) Prelude> fv (Lambda "f" (Lambda "x" (App (Var "f") (App (App (Var "t") (Var "g")) (Var "g"))))) ["t","g"]

Consider the following Haskell datatypes representing sugared and unsugared calculus terms. data PureLC = Lambda String PureLC | App PureLC PureLC | Var String deriving Show data SugaredLC = Lambdas [String] SugaredLC | Apps [SugaredLC] | Vars String deriving Show Write fv:: PurelC [ String ] desugar :: SugaredLC PurelC which finds a list of the free variables in a pure calculus term, and de-sugars a sugared calculus term, respectively. So for example Prelude> desugar (LambdaS ["f", "x"] (Apps [(Vars "f"), Apps [Vars "t", Vars "g", Vars "g"]])) Lambda "f" (Lambda "x" (App (Var "f") (App (App (Var "t") (Var "g")) (Var "g")))) Prelude> fv (Lambda "f" (Lambda "x" (App (Var "f") (App (App (Var "t") (Var "g")) (Var "g"))))) ["t", "g"]