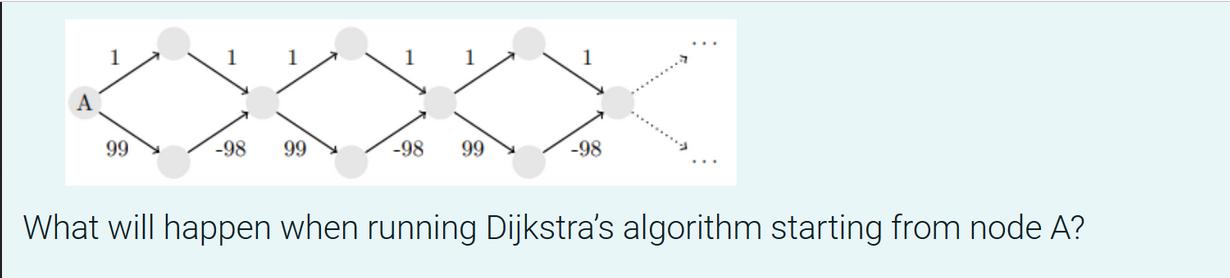
Consider the following implementation of Dijkstra's algorithm: vector graph: :get_distances (node_t source) const { vector distances (neighbors.size(), infinity); typedef pair q_entry; } priority_queue q; distances [source] = 0; q.push (make_pair (0, source)); while (!q. empty()) { q_entry next = q.top(); q.pop(); if (next.first > distances [next.second]) continue; for (neighbor n: neighbors [next.second]) { distance_t new_dist = next.first + n.distance; if (new_dist < distances [n.node]) { distances [n.node] = new_dist; q.push (make_pair (new_dist, n. node)); } } return distances; Consider further the following graph, which contains edges with negative weights, and more nodes and edges than shown, repeating the pattern: 99 -98 99 -98 99 -98 What will happen when running Dijkstra's algorithm starting from node A?