Consider the following linear program.

Maximise total profit ($) = 3X₁ + 4X₂

Subject to constraints:

X₁+3X₂ ? 12 (constraint 1)

2X₁+X₂ ? 8 (constraint 2)

X₁ ? 3 (constraint 3)

X₁, X₂ ? 0.

The following solution output is provided:

1. What is the optimal solution, and what is the value of the objective function? (You must show your workings).
2. Which constraints are binding? Justify your answer.
3. Suppose the profit on X₂ is increased to $10, is the above solution still optimal? Explain your reasoning.
4. What is the optimal objective function value if the right-hand side of the second constraint is decreased to 6? (You must show your workings).

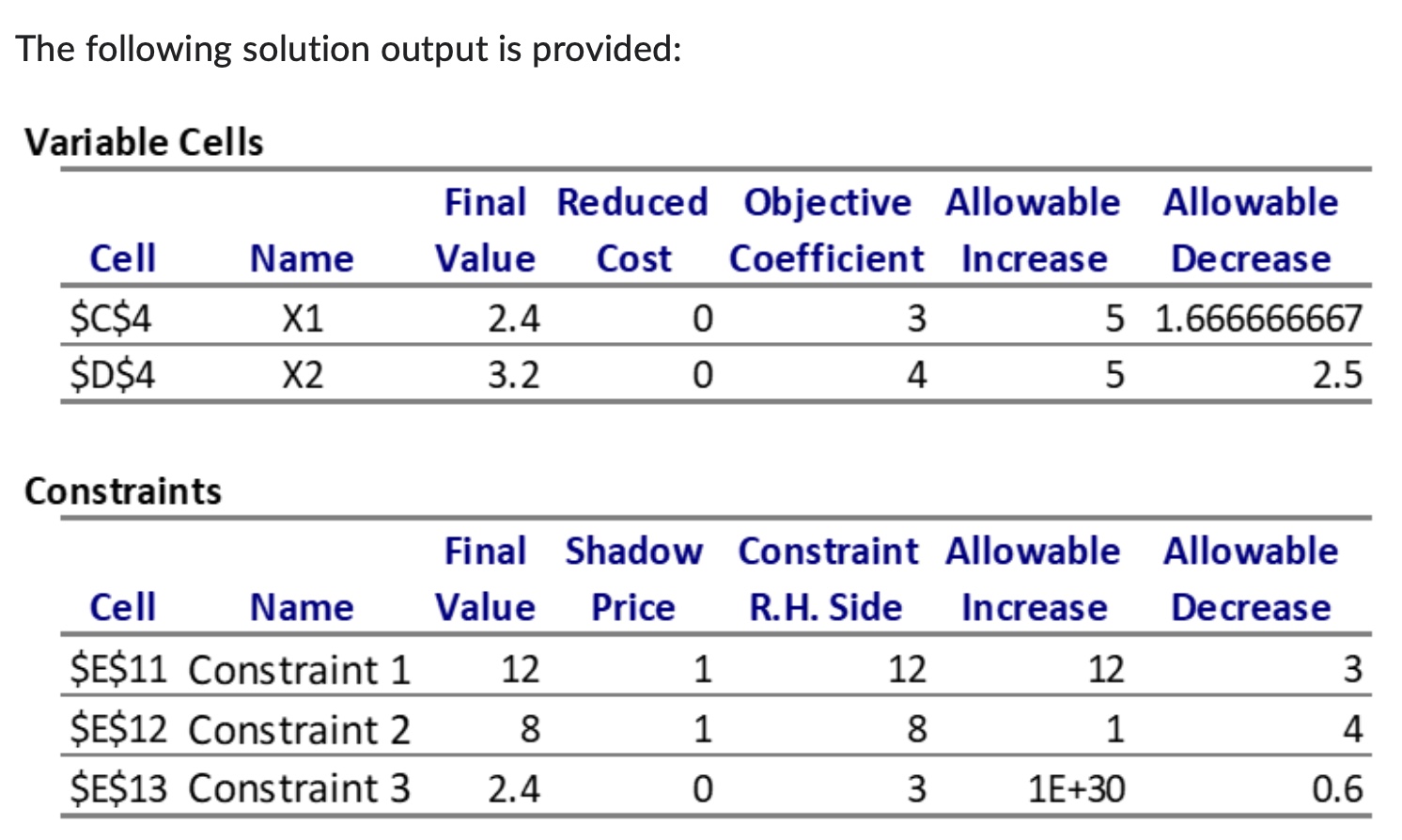
The following solution output is provided: Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $C$4 X1 2.4 0 3 5 1.666666667 $D$4 X2 3.2 0 4 5 2.5 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $E$11 Constraint 1 12 1 12 12 3 $E$12 ConstraintZ 8 1 8 1 4 $E$13 Constraint 3 2.4 O 3 1E+30 0.6