Question: Consider the following linear program. Min 8 x + 1 2 Y s . t . 1 x + 3 y 6 2 x +
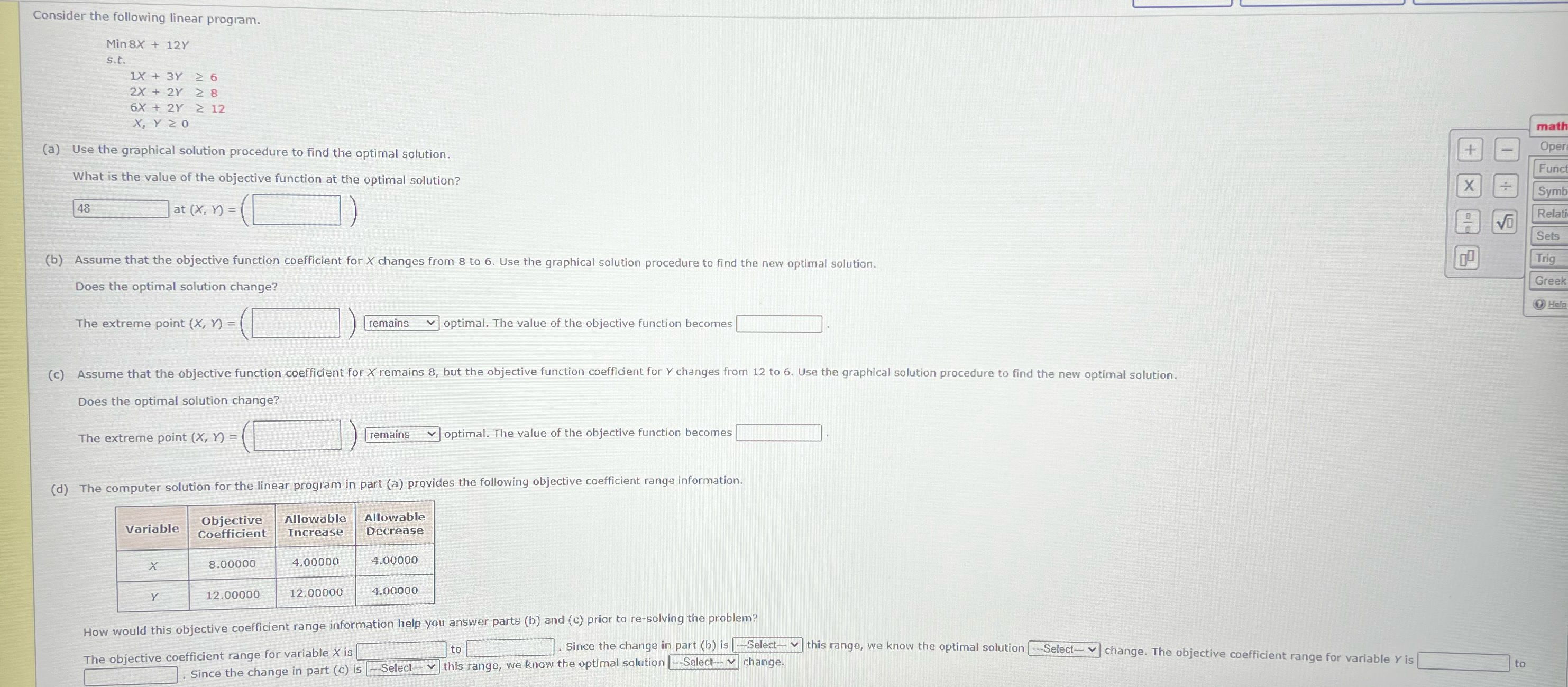
Consider the following linear program.
Min
a Use the graphical solution procedure to find the optimal solution.
What is the value of the objective function at the optimal solution?
b Assume that the objective function coefficient for changes from to Use the graphical solution procedure to find the new optimal solution. Does the optimal solution change?
The extreme point remains optimal. The value the objective function becomes
Does the optimal solution change?
d The computer solution for the linear program in part a provides the following objective coefficient range information.
tableVariabletableObjectiveCoefficienttableAllowableIncreasetableAllowableDecrease
How would this objective coefficient range information help you answer parts b and c prior to resolving the problem?
The objective coefficient range for variable is to Since the change in part b is Select this range, we know the optimal solution Select change. The objective coefficient range for variable is Since the change in part c is Select this range, we know the optimal solution Select change.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


