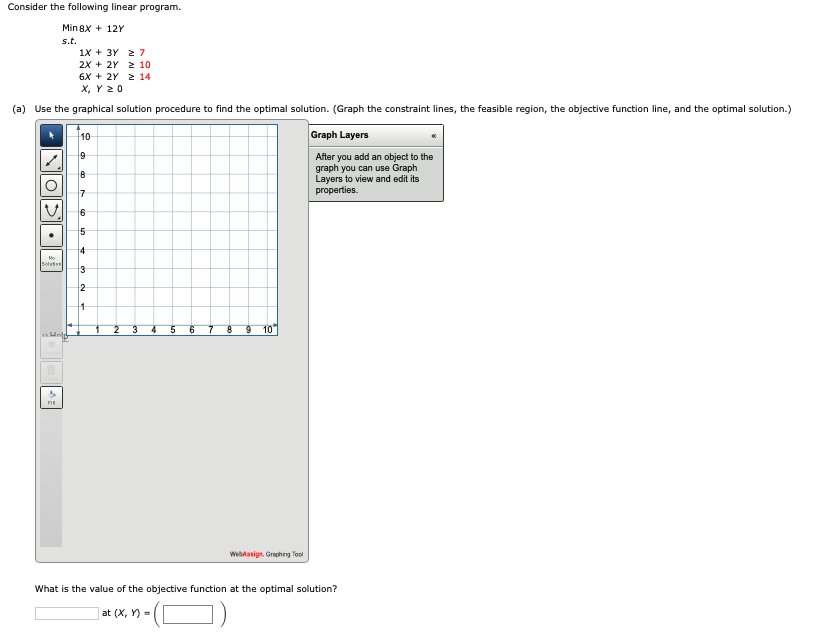
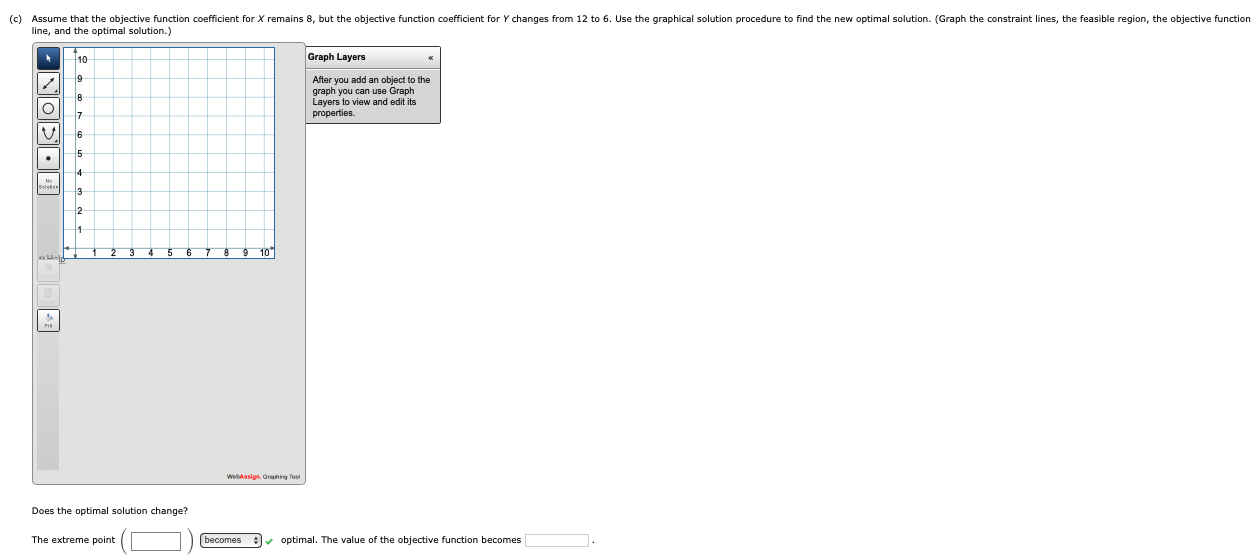
Consider the following linear program. Min 8X + 12Y s.t. 1X + 3Y 27 2X + 2Y = 10 6X + 2y = 14 X, Y 20 (a) Use the graphical solution procedure to find the optimal solution. (Graph the constraint lines, the feasible region, the objective function line, and the optimal solution.) 10 Graph Layers After you add an object to the graph you can use Graph Layers to view and edit its properties. 9 8 7 6 5 4 Bos 3 2 1 8 9 10 WebAssign, Graphing Tool What is the value of the objective function at the optimal solution? at (x, y) = (b) Assume that the objective function coefficient for X changes from 8 to 6. Use the graphical solution procedure to find the new optimal solution. (Graph the constraint lines, the feasible region, the objective function line, and the optimal solution.) 110 19 Graph Layers After you add an object to the graph you can use Graph Layers to view and edit its properties 7 NODO V 16 15 6 7 8 9 10 WebAssis. Gruphing Tool Does the optimal solution change? The extreme point remains optimal. The value of the objective function becomes (c) Assume that the objective function coefficient for X remains 8, but the objective function coefficient for Y changes from 12 to 6. Use the graphical solution procedure line, and the optimal solution.) find the new optimal solution. (Graph the constraint lines, the feasible region, the objective function 10 Graph Layers After you add an object to the graph you can use Graph Layers to view and edit its properties O NOPOD V 5 13 WebAssign Graphing Too Does the optimal solution change? The extreme point becomes optimal. The value of the objective function becomes (d) The computer solution for the linear program in part (a) provides the following objective coefficient range information. Variable Objective Coefficient Allowable Increase Allowable Decrease X 8.00000 4.00000 4.00000 Y 12.00000 12.00000 4.00000 How would this objective coefficient range information help you answer parts (b) and (c) prior to re-solving the problem? The objective coefficient range for variable X is 1. Since the change in part (b) is within 1. Since the change in part (c) is outside this range, we know the optimal solution will to change. The objective coefficient range for variable Y is this range, we know the optimal solution will not change