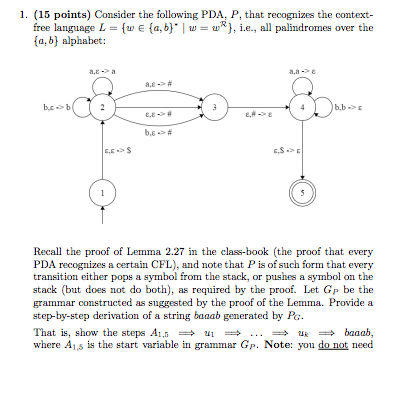
Consider the following PDA, P, that recognizes the context free language L = {w element (a, b) | w = w^R}, i.e., all palindromes over the {a, b} alphabet: Recall the proof of Lemma 2.27 in the class-book (the proof that every PDA recognizes a certain CFL), and note that P is of such form that every transition either pops a symbol from the stack, or pushes a symbol on the stack (but does not do both), as required by the proof. Let G_P be the grammar constructed as suggested by the proof of the Lemma. Provide a step-by-step derivation of a string baaab generated by PG That is, show the steps baaab. where A_1, 5 is the start variable in grammar Gp