Consider the following problem:

Maximize: Z = 4x1 + 3x2 + x3 + 2x4 s.t.: 4x1 + 2x2 + x3 + x4 5 3x1 + x2 + 2x3 + x4 4 Where: x1, x2, x3, x4 0

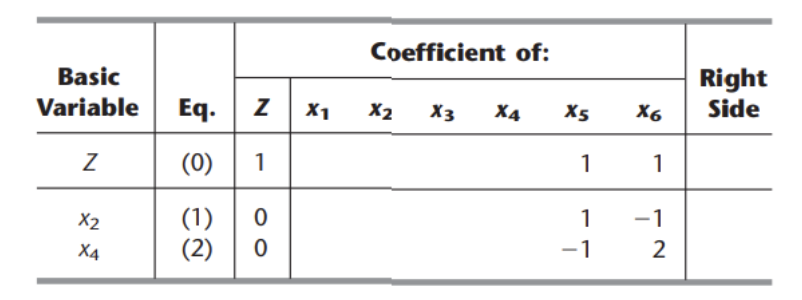
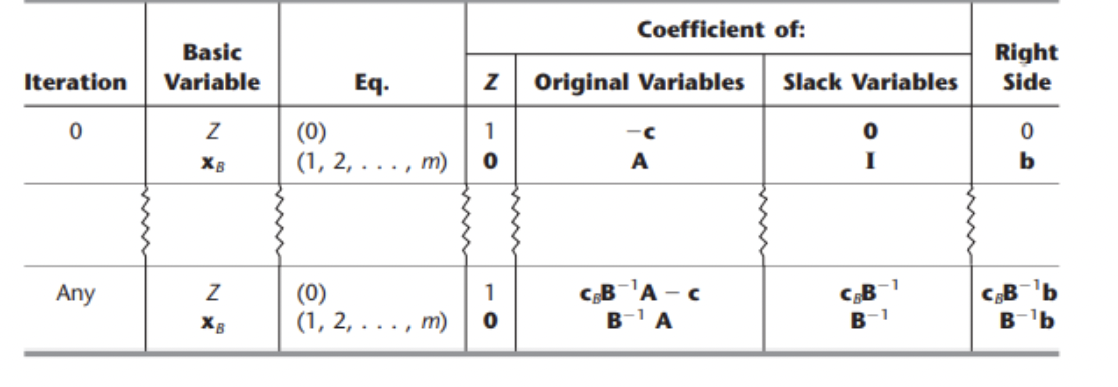
a) Using the matrix representation of the standard form linear program, derive the fundamental insight described by the table below, assuming that we have n decision variables and m functional constraints.

(b) Use the table in part (a) to fill in the rest of the final tableau. (c) Identify the defining equations of the corner point feasible solution corresponding to the optimal basic feasible solution in the final simplex tableau.

Coefficient of: Basic Variable Right Side Eq. N z X1 X2 X3 X4 X5 X6 Z (0) 1 1 1 X2 (1) (2) 0 0 1 1 -1 2 X4 Basic Variable Right Side Eq. Iteration 0 Coefficient of: z Original Variables Slack Variables 0 A I 1 -C Z XB (0) (1, 2, ...,m) o 0 b Any 1 (0) (1, 2, : CB-A-C B-A CB-1 O- CB-'b B-b XB m) B-1