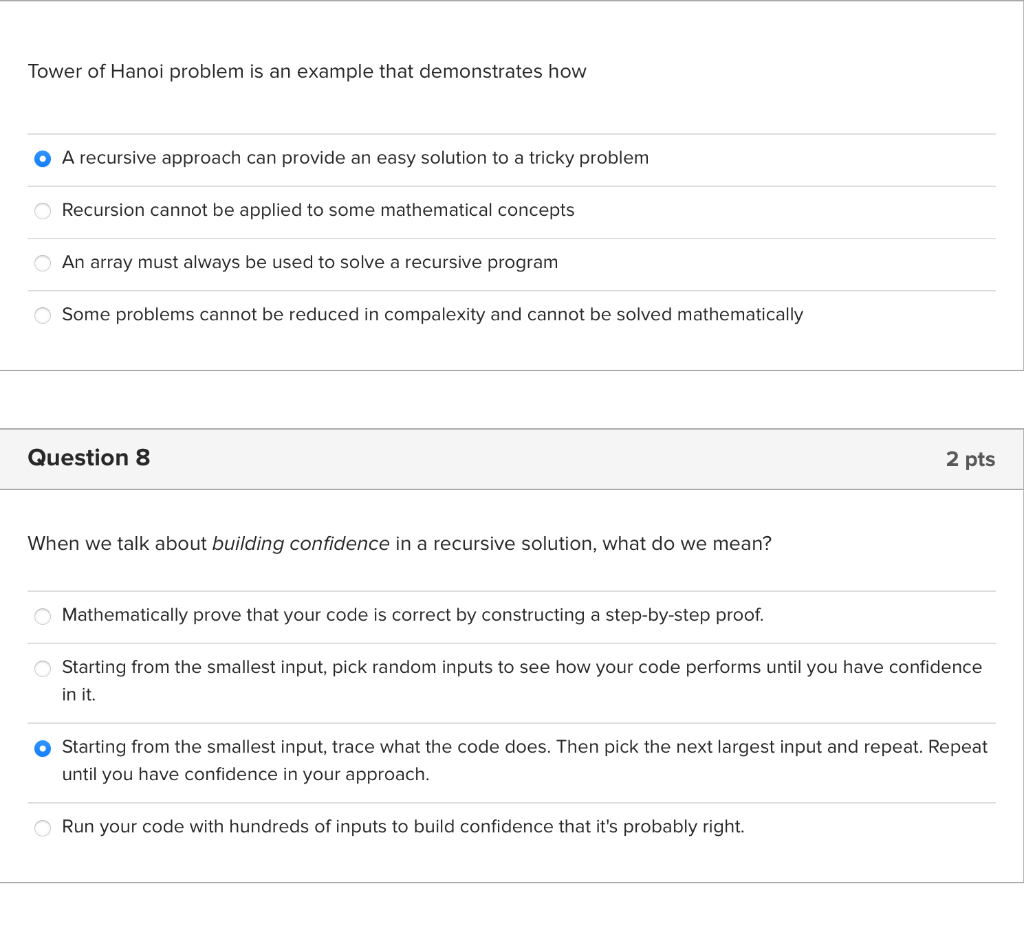
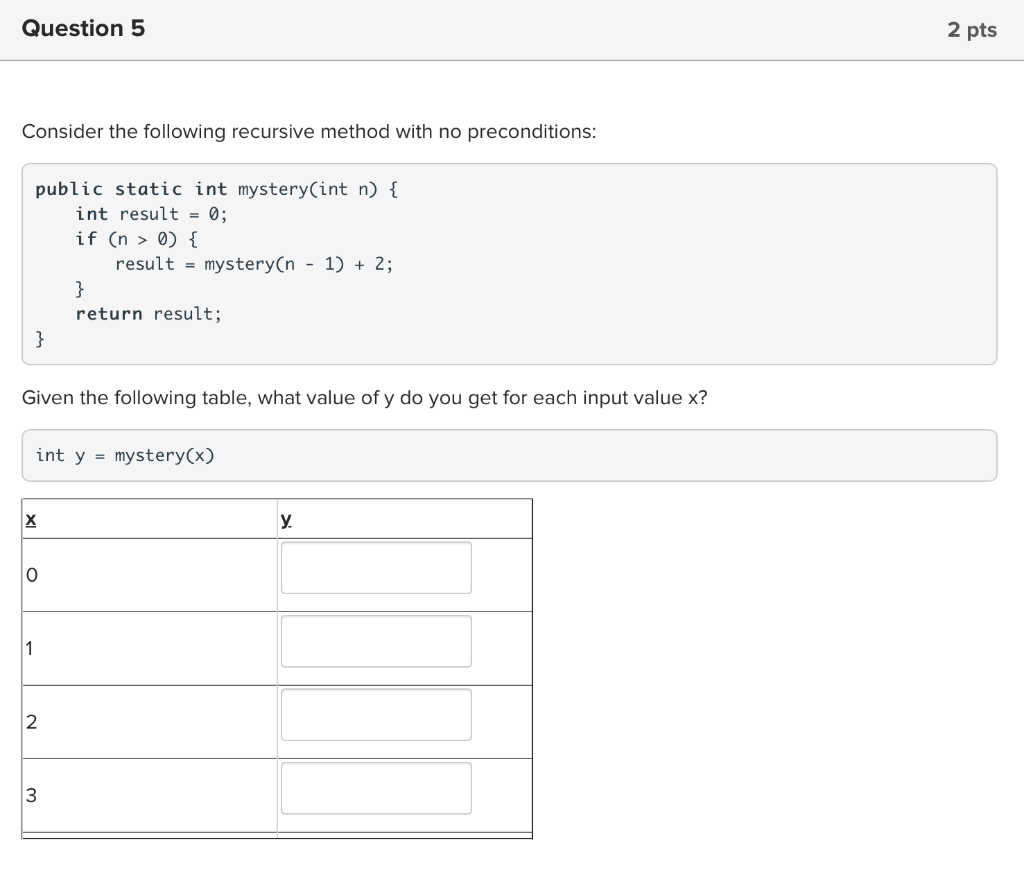
Consider the following recursive method implementation public static int enigma(int[] a, int start, int end) { int result = end; if ( start a[start] ) { result = index; } else { result = start; } } return result; } What values for start and end would cause this method to execute its base case? start = 2, end = 2 start = 6, end = 2 start = 2, end = 6 Question 5 2 pts Consider the following recursive method with no preconditions: public static int mystery(int n) { int result = 0; if (n > 0) { result = mystery(n - 1) + 2; } return result; } Given the following table, what value of y do you get for each input value x? int y = mystery(x) X y. 0 1 2 3 Consider the following recursive method implementation public static int enigma(int[] a, int start, int end) { int result = end; if ( start a[start] ) { result = index; } else { result = start; } } return result; } What values for start and end would cause this method to execute its base case? start = 2, end = 2 start = 6, end = 2 start = 2, end = 6 Tower of Hanoi problem is an example that demonstrates how O A recursive approach can provide an easy solution to a tricky problem Recursion cannot be applied to some mathematical concepts An array must always be used to solve a recursive program Some problems cannot be reduced in compalexity and cannot be solved mathematically Question 8 2 pts When we talk about building confidence in a recursive solution, what do we mean? O Mathematically prove that your code is correct by constructing a step-by-step proof. Starting from the smallest input, pick random inputs to see how your code performs until you have confidence in it. Starting from the smallest input, trace what the code does. Then pick the next largest input and repeat. Repeat until you have confidence in your approach. Run your code with hundreds of inputs to build confidence that it's probably right