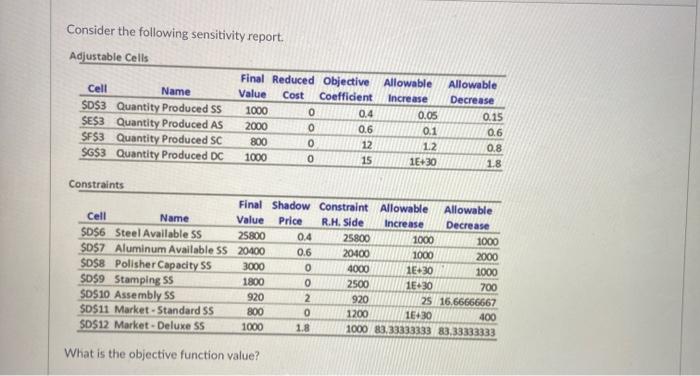
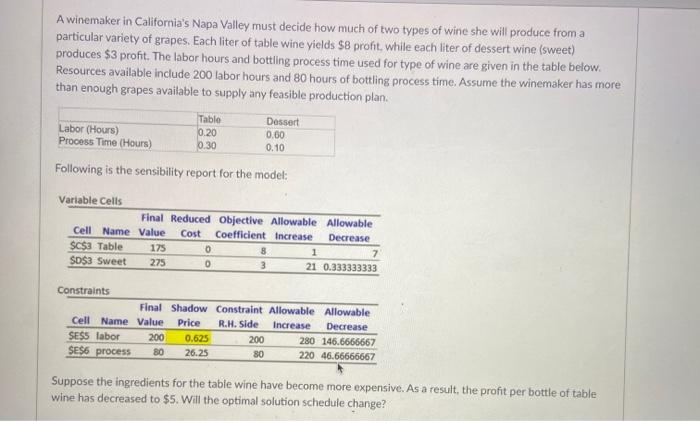
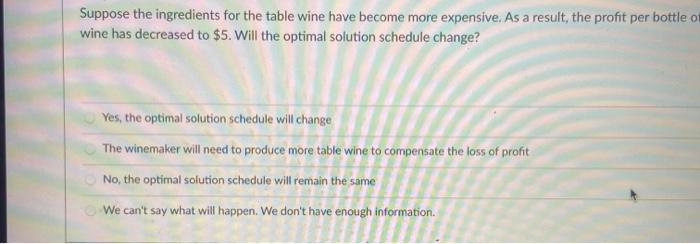
Consider the following sensitivity report. Adjustable Cells Cell Name $D$3 Quantity Produced SS $E$3 Quantity Produced AS SF$3 Quantity Produced SC $G$3 Quantity Produced DC Final Reduced Objective Allowable Value Cost Coefficient Increase 1000 0 0.4 0.05 2000 0 0.6 0.1 800 0 12 12 1000 0 15 15.30 Allowable Decrease 0.15 0.6 0.8 1.8 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $D$6 Steel Available ss 25800 0.4 25800 1000 1000 $D$7 Aluminum Available SS 20400 0.6 20400 1000 2000 SD$8 Polisher Capacity S5 3000 0 4000 1E30 1000 $D$9 Stamping 55 1800 2500 15.30 700 $0$10 Assembly SS 920 2 920 25 16.66666667 $D$11 Market - Standard SS 800 1200 1E430 400 $D$12 Market - Deluxe 55 1000 1.8 1000 83.33333333 83.33333333 ONO What is the objective function value? A winemaker in California's Napa Valley must decide how much of two types of wine she will produce from a particular variety of grapes. Each liter of table wine yields $8 profit, while each liter of dessert wine (sweet) produces $3 profit. The labor hours and bottling process time used for type of wine are given in the table below. Resources available include 200 labor hours and 80 hours of bottling process time. Assume the winemaker has more than enough grapes available to supply any feasible production plan. Labor (Hours) Process Time (Hours) Table 0.20 0.30 Dessert 0.60 0.10 Following is the sensibility report for the model: Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient increase Decrease $C$3 Table 175 0 8 1 7 SD$3 Sweet 275 0 3 21 0.333333333 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease SESS labor 200 0.625 200 280 146.6666667 $E$6 process 80 26.25 80 220 46.66666667 Suppose the ingredients for the table wine have become more expensive. As a result, the profit per bottle of table wine has decreased to $5. Will the optimal solution schedule change? Suppose the ingredients for the table wine have become more expensive. As a result, the profit per bottle o wine has decreased to $5. Will the optimal solution schedule change? Yes, the optimal solution schedule will change The winemaker will need to produce more table wine to compensate the loss of profit No, the optimal solution schedule will remain the same We can't say what will happen. We don't have enough information Consider the following sensitivity report. Adjustable Cells Cell Name $D$3 Quantity Produced SS $E$3 Quantity Produced AS SF$3 Quantity Produced SC $G$3 Quantity Produced DC Final Reduced Objective Allowable Value Cost Coefficient Increase 1000 0 0.4 0.05 2000 0 0.6 0.1 800 0 12 12 1000 0 15 15.30 Allowable Decrease 0.15 0.6 0.8 1.8 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $D$6 Steel Available ss 25800 0.4 25800 1000 1000 $D$7 Aluminum Available SS 20400 0.6 20400 1000 2000 SD$8 Polisher Capacity S5 3000 0 4000 1E30 1000 $D$9 Stamping 55 1800 2500 15.30 700 $0$10 Assembly SS 920 2 920 25 16.66666667 $D$11 Market - Standard SS 800 1200 1E430 400 $D$12 Market - Deluxe 55 1000 1.8 1000 83.33333333 83.33333333 ONO What is the objective function value? A winemaker in California's Napa Valley must decide how much of two types of wine she will produce from a particular variety of grapes. Each liter of table wine yields $8 profit, while each liter of dessert wine (sweet) produces $3 profit. The labor hours and bottling process time used for type of wine are given in the table below. Resources available include 200 labor hours and 80 hours of bottling process time. Assume the winemaker has more than enough grapes available to supply any feasible production plan. Labor (Hours) Process Time (Hours) Table 0.20 0.30 Dessert 0.60 0.10 Following is the sensibility report for the model: Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient increase Decrease $C$3 Table 175 0 8 1 7 SD$3 Sweet 275 0 3 21 0.333333333 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease SESS labor 200 0.625 200 280 146.6666667 $E$6 process 80 26.25 80 220 46.66666667 Suppose the ingredients for the table wine have become more expensive. As a result, the profit per bottle of table wine has decreased to $5. Will the optimal solution schedule change? Suppose the ingredients for the table wine have become more expensive. As a result, the profit per bottle o wine has decreased to $5. Will the optimal solution schedule change? Yes, the optimal solution schedule will change The winemaker will need to produce more table wine to compensate the loss of profit No, the optimal solution schedule will remain the same We can't say what will happen. We don't have enough information