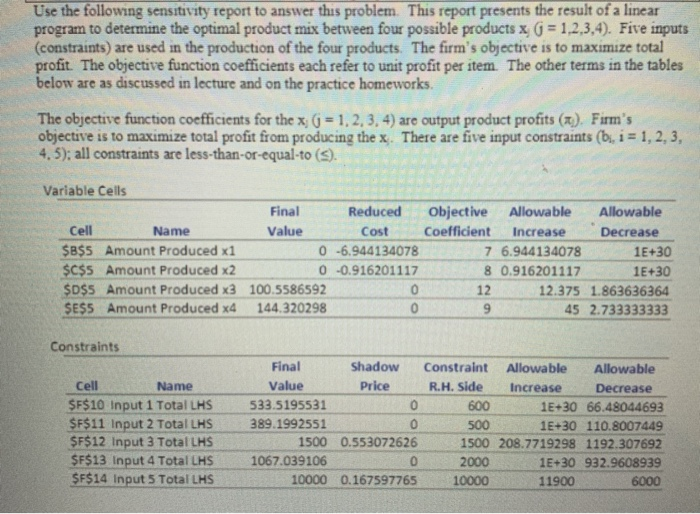
Question: Use the following sensitivity report to answer this problem. This report presents the result of a linear program to determine the optimal product mix between
Use the following sensitivity report to answer this problem. This report presents the result of a linear program to determine the optimal product mix between four possible products x G = 1,2,3,4). Five inputs (constraints) are used in the production of the four products. The firm's objective is to maximize total profit. The objective function coefficients each refer to unit profit per item. The other terms in the tables below are as discussed in lecture and on the practice homeworks. The objective function coefficients for the x; 6 = 1, 2, 3, 4) are output product profits (13). Firm's objective is to maximize total profit from producing the x. There are five input constraints (bi, i = 1, 2, 3, 4.5): all constraints are less-than-or-equal-to (3). Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase . Decrease $B$5 Amount Produced x1 0 -6.944134078 7 6.944134078 1 E+30 $C$5 Amount Produced x2 0 -0.916201117 8 0.916201117 1 E+30 $D$5 Amount Produced x3 100.5586592 12.375 1.863636364 $E$5 Amount Produced x4 144.320298 45 2.733333333 Constraints Cell Name $F$10 Input 1 Total LHS $F$11 Input 2 Total LHS $F$12 Input 3 Total LHS $F$13 Input 4 Total LHS $F$14 Input 5 Total LHS Final Shadow Value Price 533.5195531 389.1992551 1500 0.553072626 1067.039106 10000 0.167597765 Constraint Allowable Allowable R.H. Side Increase Decrease 600 1 E+30 66.48044693 500 1E+30 110.8007449 1500 208.7719298 1192.307692 2000 1E+30 932.9608939 10000 11900 6000 You are given the following primal LP, where the x are outputs, the P are output prices and the constraints are input availabilities: max TR = 12x + 2x: - Sx; -20 3x - 2x: + 8x - 4x4 S 100 4x2 - 6x - 5x 2x225 X 20 ( = 1,2,3,4) Given here is the Solver Sensitivity Analysis with some of the entries omitted. Variable Cells Cell Name $D$4 Amount Produced x1 SES4 Amount Produced x2 $E$4 Amount Produced x3 $G$4 Amount Produced x4 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 3 123 1E+30 ? 1E+30 ? 201E+304 1E+30 Constraints Cell Name $H$8 Constraint 1 Total LHS $H$9 Constraint 2 Total LHS Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease ? 5 100 1E+3050 ? 0 25 2 5 1530 Use the following sensitivity report to answer this problem. This report presents the result of a linear program to determine the optimal product mix between four possible products x G = 1,2,3,4). Five inputs (constraints) are used in the production of the four products. The firm's objective is to maximize total profit. The objective function coefficients each refer to unit profit per item. The other terms in the tables below are as discussed in lecture and on the practice homeworks. The objective function coefficients for the x; 6 = 1, 2, 3, 4) are output product profits (13). Firm's objective is to maximize total profit from producing the x. There are five input constraints (bi, i = 1, 2, 3, 4.5): all constraints are less-than-or-equal-to (3). Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase . Decrease $B$5 Amount Produced x1 0 -6.944134078 7 6.944134078 1 E+30 $C$5 Amount Produced x2 0 -0.916201117 8 0.916201117 1 E+30 $D$5 Amount Produced x3 100.5586592 12.375 1.863636364 $E$5 Amount Produced x4 144.320298 45 2.733333333 Constraints Cell Name $F$10 Input 1 Total LHS $F$11 Input 2 Total LHS $F$12 Input 3 Total LHS $F$13 Input 4 Total LHS $F$14 Input 5 Total LHS Final Shadow Value Price 533.5195531 389.1992551 1500 0.553072626 1067.039106 10000 0.167597765 Constraint Allowable Allowable R.H. Side Increase Decrease 600 1 E+30 66.48044693 500 1E+30 110.8007449 1500 208.7719298 1192.307692 2000 1E+30 932.9608939 10000 11900 6000 You are given the following primal LP, where the x are outputs, the P are output prices and the constraints are input availabilities: max TR = 12x + 2x: - Sx; -20 3x - 2x: + 8x - 4x4 S 100 4x2 - 6x - 5x 2x225 X 20 ( = 1,2,3,4) Given here is the Solver Sensitivity Analysis with some of the entries omitted. Variable Cells Cell Name $D$4 Amount Produced x1 SES4 Amount Produced x2 $E$4 Amount Produced x3 $G$4 Amount Produced x4 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 3 123 1E+30 ? 1E+30 ? 201E+304 1E+30 Constraints Cell Name $H$8 Constraint 1 Total LHS $H$9 Constraint 2 Total LHS Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease ? 5 100 1E+3050 ? 0 25 2 5 1530