Consider the following sets representing computational problems

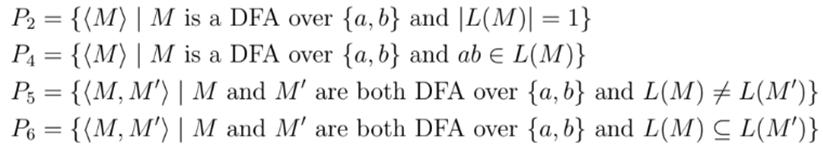
Prove that each of these four problems is decidable

P = {(M) | M is a DFA over {a,b} and |L(M)| = 1} P = {(M) | M is a DFA over {a,b} and ab L(M)} P5 = {(M, M') | M and M' are both DFA over {a,b} and L(M) L(M')} P6 = {(M, M') | M and M' are both DFA over {a, b} and L(M) L(M')}