Consider the following simultaneous-move game between two players:

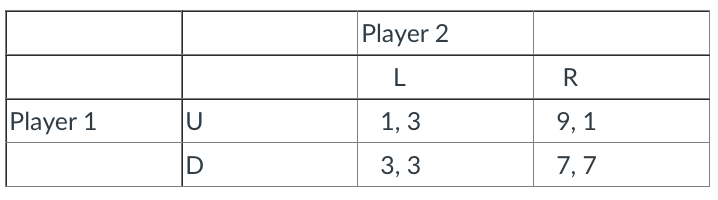
a) Find the Nash equilibria in the game (in pure and mixed strategies) and the associated payoffs for the players.

b) Now assume that the game is extended in the following way: in the beginning Player 1 can decide whether to opt out (this choice is denoted by O) or whether to play the simultaneous-move game in a) (this choice is denoted by G). If Player 1 opts out (plays O) then both Player 1 and Player 2 get a payoff of 4 each and the game ends. If Player 1 decides to play G, then the simultaneous-move game is played. Find the pure-strategy Nash equilibria in this extended version of the game. (Hint: note that Player 1 now has 4 strategies and write the game up in a 4x2 matrix.)

c) Write the game in (b) up in extensive form (a game tree). Identify the subgames of this game.

d) Which, if any, of the pure-strategy Nash equilibria you identified in (c) are subgame perfect?

e) Find the unique subgame-perfect Nash equilibrium of the game. (Hint: Player 1 will choose his first move so as to maximize his expected payoff.)

\begin{tabular}{|l|l|c|l|} \hline & \multicolumn{2}{|c|}{ Player 2 } & \\ \hline & & L & R \\ \hline Player 1 & U & 1,3 & 9,1 \\ \hline & D & 3,3 & 7,7 \\ \hline \end{tabular}