Consider the following syntax for a term in the "unsugared" untyped calculus, represented as an s-expression: E ::= ( V E) | (E E) | V.where V is a variable.

For example, the term fx.f(tgg) would be de-sugared to f.x.f((tg)g) and then represented as the s-expression ( f ( x (f ((t g) g)))). Write a scheme function fv which takes an s-expression of this sort, and returns a list of the free variables. E.g,

(fv '( f ( x (f ((t g) g)))))  (t g) 

or (g t). Hint: you may want to write a function to take the union of two sets represented as lists of elements, and a function to remove a given element from a set.

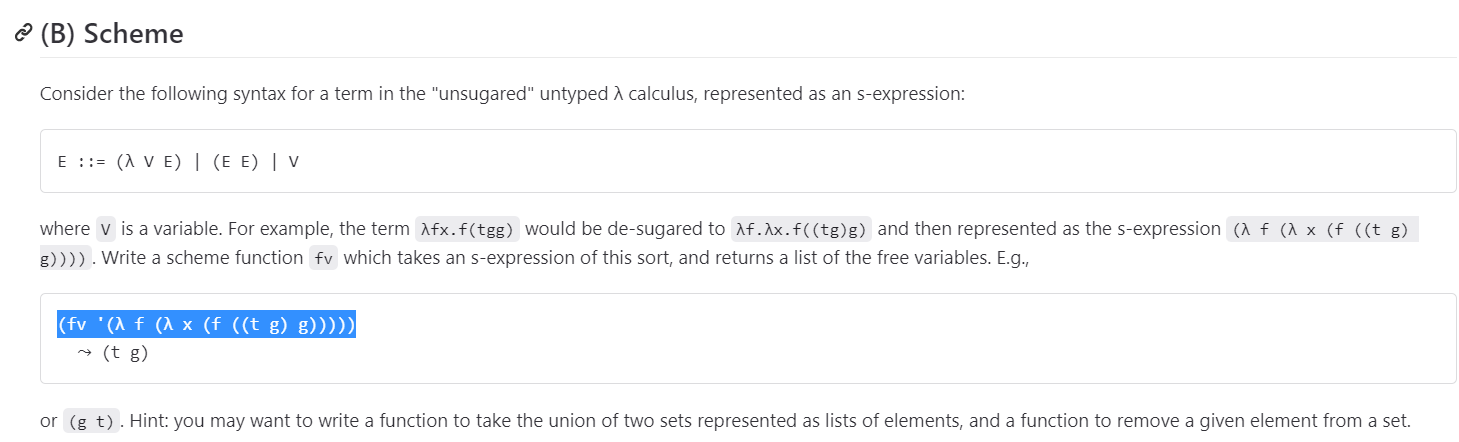
Consider the following syntax for a term in the "unsugared" untyped calculus, represented as an s-expression: E::=(E)(EE)V where v is a variable. For example, the term would be de-sugared to and then represented as the s-expression (f((f)(tg) g)) )). Write a scheme function fv which takes an s-expression of this sort, and returns a list of the free variables. E.g