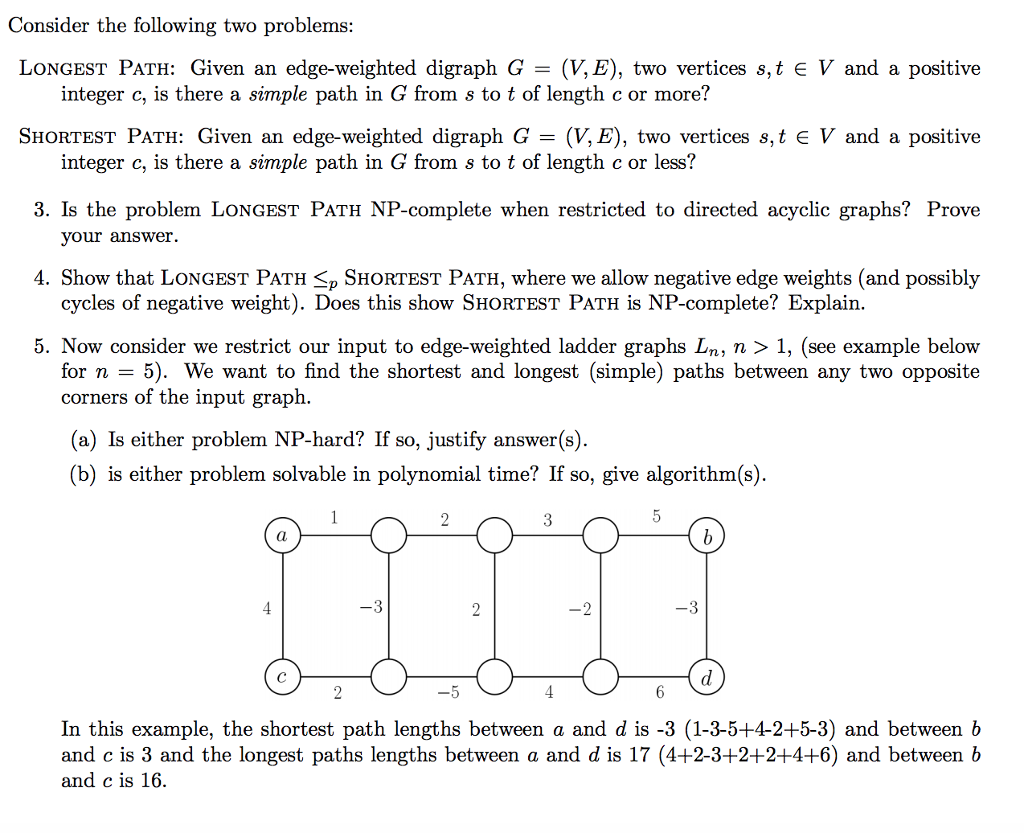
Consider the following two problems: LONGEST PATH: Given an edge-weighted digraph G = (V,E), two vertices s, t E V and a positive integer c, is there a simple path in G from s to t of length c or more? ShOrTeST PATH: Given an edge-weighted digraph G-(V, E), two vertices s,t V and a positive integer c, is there a simple path in G from s to t of length c or less? 3. Is the problem LongesT PATh NP-complete when restricted to directed acyclic graphs? Prove 4. Show that LONGEST PATH

1, (see example below youranswer. cycles of negative weight). Does this show SHORTEST PATH is NP-complete? Explain. for n -5). We want to find the shortest and longest (simple) paths between any two opposite corners of the input graph. (a) Is either problem NP-hard? If so, justify answer(s) (b) is either problem solvable in polynomial time? If so, give algorithm(s) In this example, the shortest path lengths between a and d is -3 (1-3-5+4-2+5-3) and between t and c is 3 and the longest paths lengths between a and d is 17 (4+2-3+2+2+4+6) and between b and c is 16 Consider the following two problems: LONGEST PATH: Given an edge-weighted digraph G = (V,E), two vertices s, t E V and a positive integer c, is there a simple path in G from s to t of length c or more? ShOrTeST PATH: Given an edge-weighted digraph G-(V, E), two vertices s,t V and a positive integer c, is there a simple path in G from s to t of length c or less? 3. Is the problem LongesT PATh NP-complete when restricted to directed acyclic graphs? Prove 4. Show that LONGEST PATH

1, (see example below youranswer. cycles of negative weight). Does this show SHORTEST PATH is NP-complete? Explain. for n -5). We want to find the shortest and longest (simple) paths between any two opposite corners of the input graph. (a) Is either problem NP-hard? If so, justify answer(s) (b) is either problem solvable in polynomial time? If so, give algorithm(s) In this example, the shortest path lengths between a and d is -3 (1-3-5+4-2+5-3) and between t and c is 3 and the longest paths lengths between a and d is 17 (4+2-3+2+2+4+6) and between b and c is 16