Question: Consider the function defined on the indicated interval. f(x) = 3(2 + 5)3 - 22, [-6, -4] Find the maximum and minimum values. Max: Min:Find
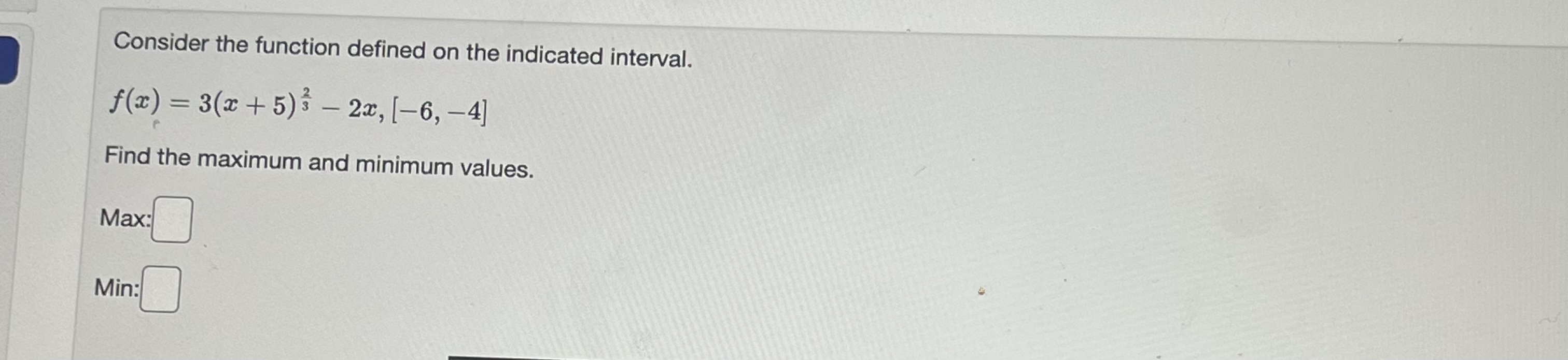
![+ 5)3 - 22, [-6, -4] Find the maximum and minimum values.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666474c6e2059_526666474c6c3701.jpg)
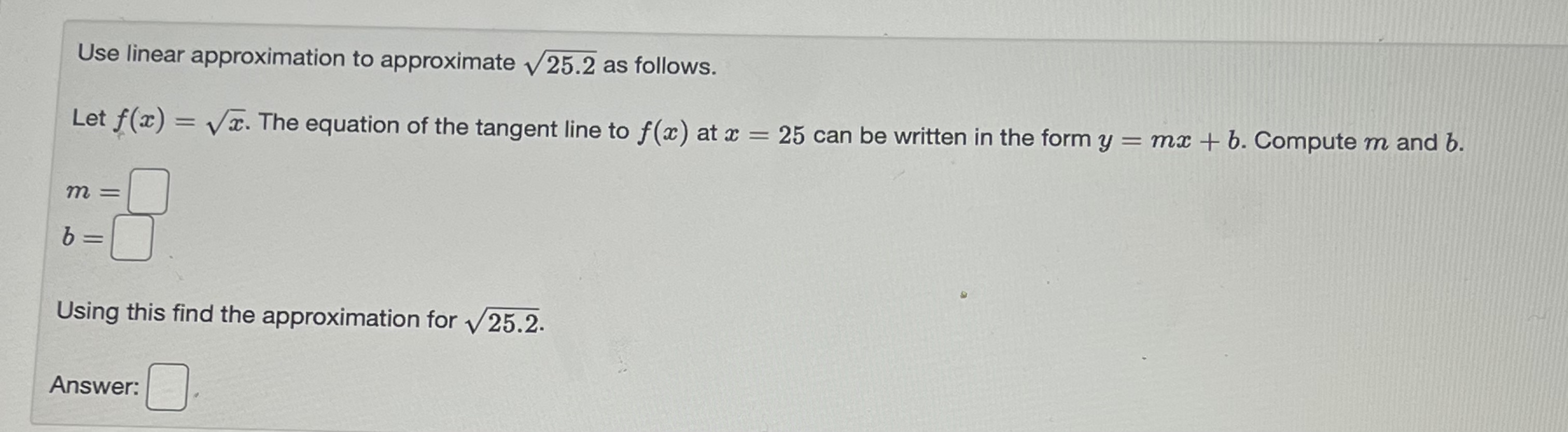

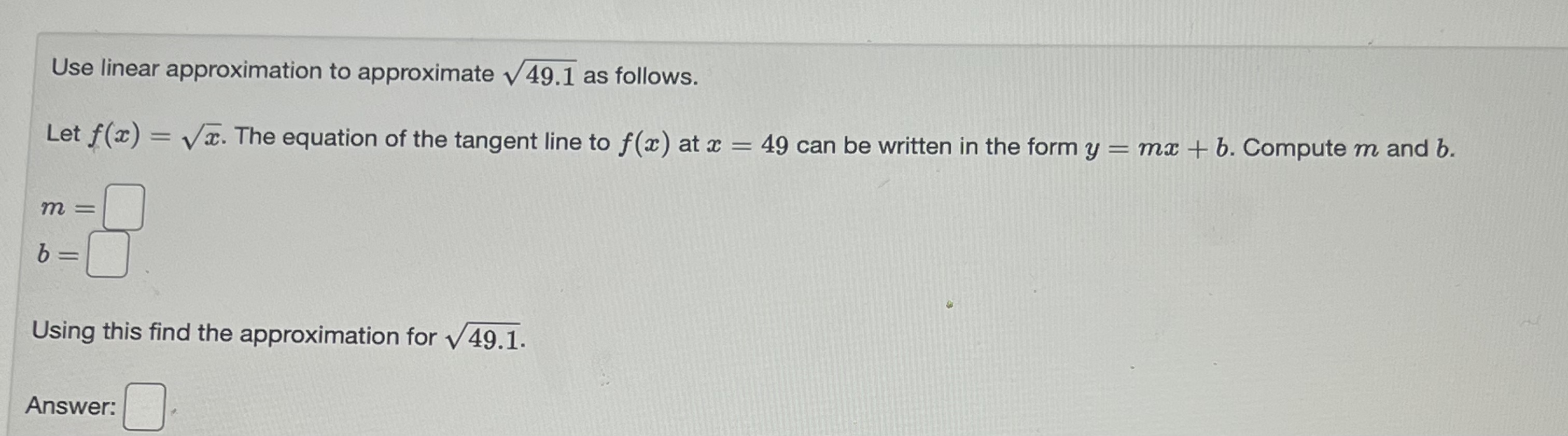

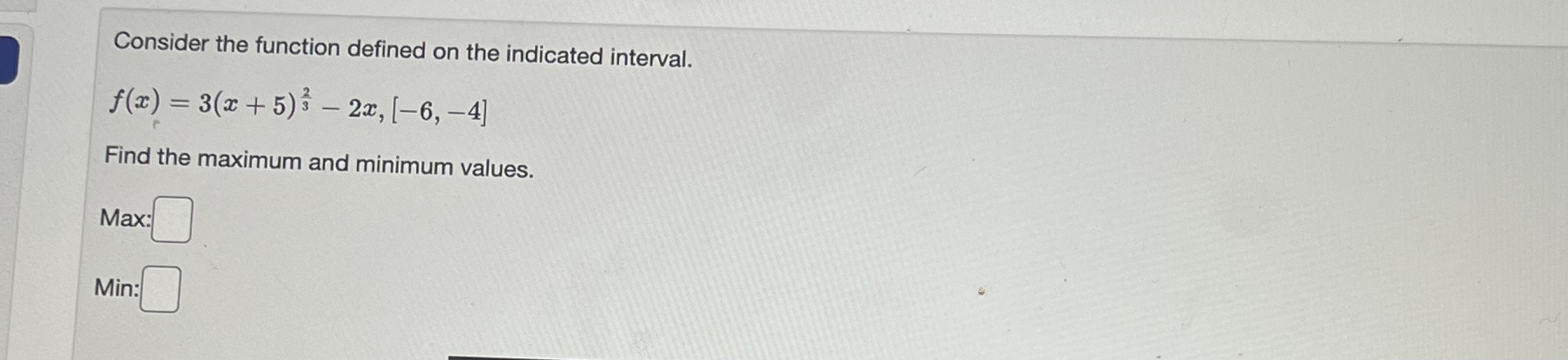
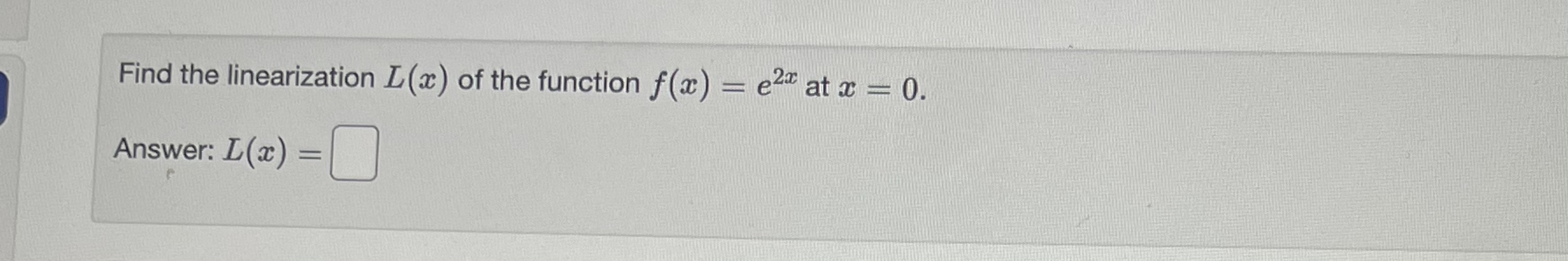
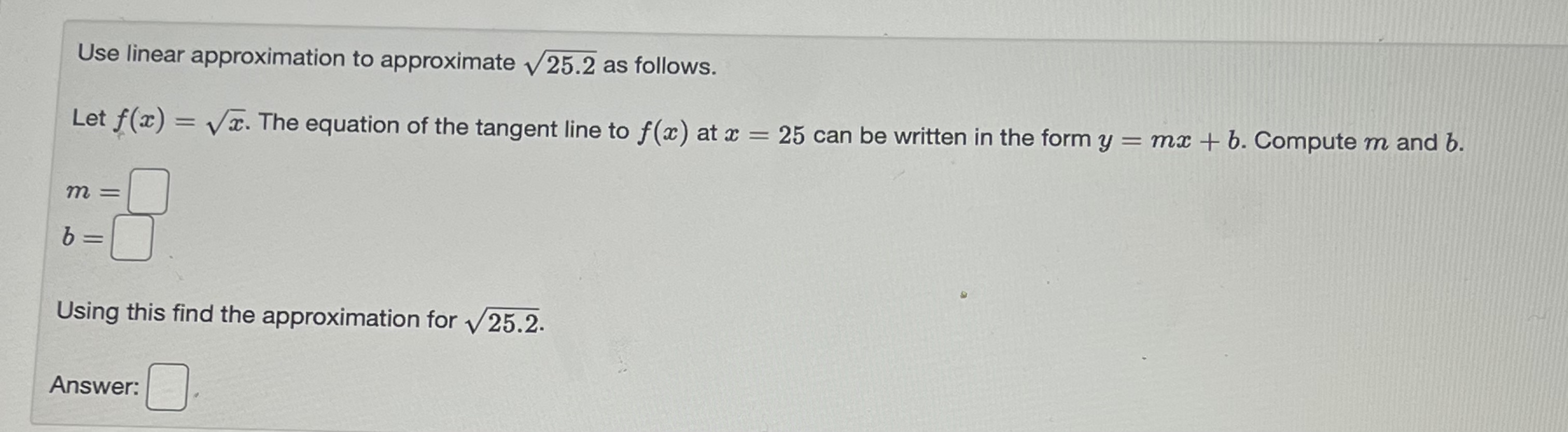

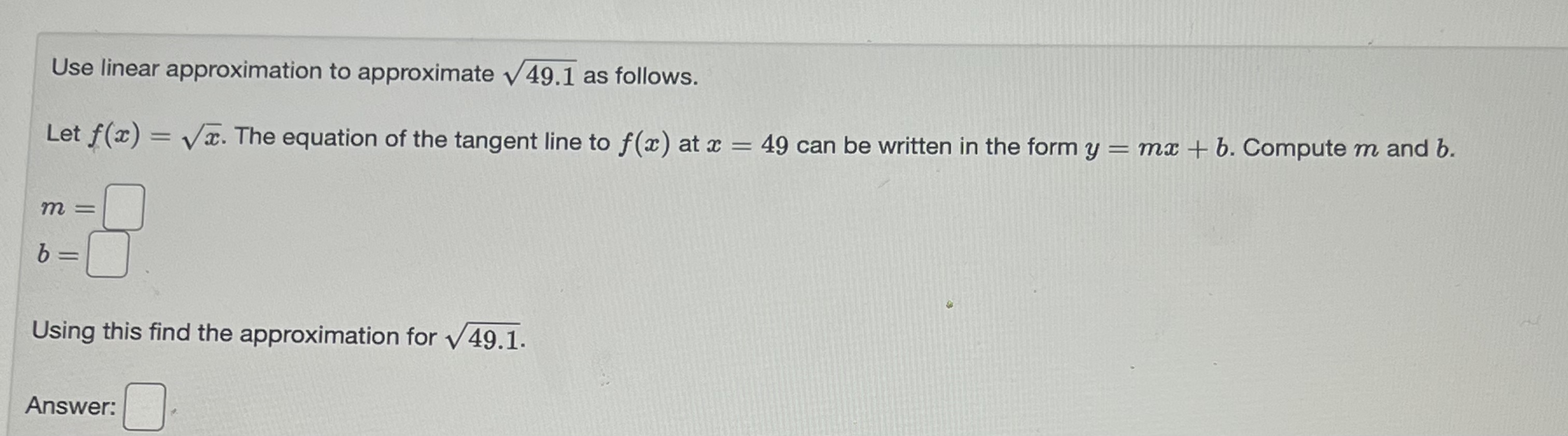

Consider the function defined on the indicated interval. f(x) = 3(2 + 5)3 - 22, [-6, -4] Find the maximum and minimum values. Max: Min:Find the linearization L(x) of the function f(x) = e27 at x - 0. Answer: L(x) =[Use linear approximation to approximate v 25.2 as follows. Let f(x) = Vx. The equation of the tangent line to f (x) at x = 25 can be written in the form y = mx + b. Compute m and b. m= b Using this find the approximation for v 25.2. Answer:Find the linear approximation of f(x) = In x at x = 1 and use it to estimate In (1.25). L(x) = In 1.25 ~Use linear approximation to approximate v 49.1 as follows. Let f(x) = Va. The equation of the tangent line to f(x) at x = 49 can be written in the form y = ma + b. Compute m and b. m b Using this find the approximation for \\ 49.1. Answer:
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


