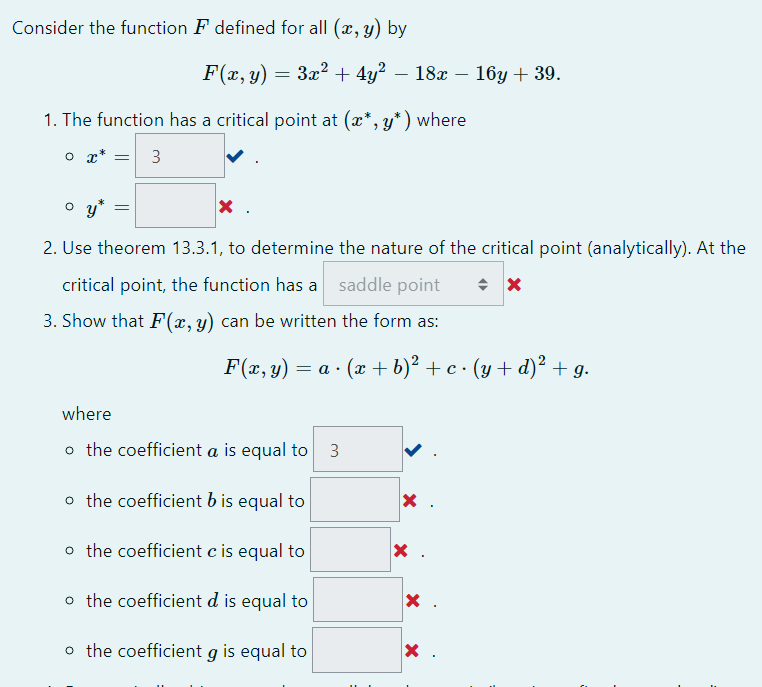
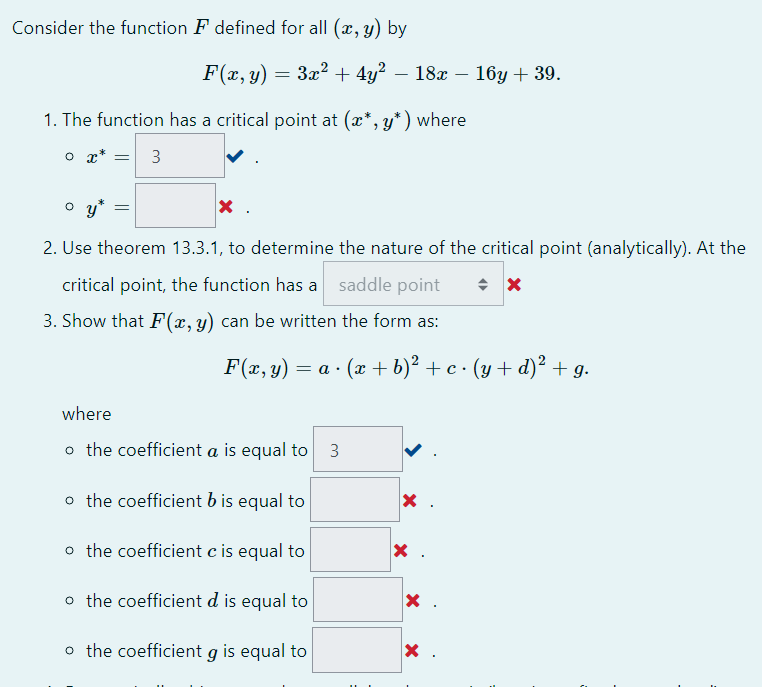
Consider the function F defined for all (x, y) by F(x, y) = 3x2 + 4y2 - 18x - 16y + 39. 1. The function has a critical point at (a*, y* ) where 3 X 2. Use theorem 13.3.1, to determine the nature of the critical point (analytically). At the critical point, the function has a saddle point X 3. Show that F(x, y) can be written the form as: F(x, y) = a . (x+b)' +c . (y+ d)'+g. where o the coefficient a is equal to 3 o the coefficient b is equal to X o the coefficient c is equal to X o the coefficient d is equal to X o the coefficient g is equal to X