Question: Consider the function f given by f(x, y, z) = xz. Find the average value of the function f over the region F in the

in the first octant bounded by the coordinate planes and the parabolic

XCertainly! Let's go ahead and compute the integral to find the average

value of the function at, 3;, z] = M over the region

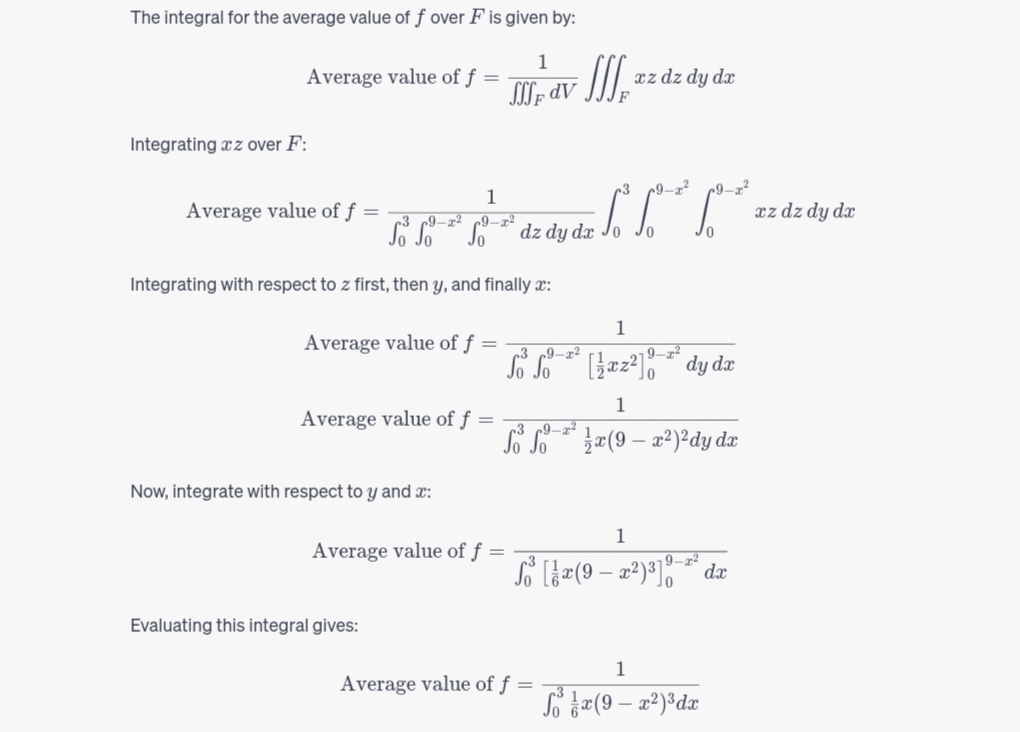
Consider the function f given by f(x, y, z) = xz. Find the average value of the function f over the region F in the first octant bounded by the coordinate planes and the parabolic cylinders z = 9 - x and y = 9 - x. XCertainly! Let's go ahead and compute the integral to find the average value of the function at, 3;, z] = M over the region F in the first octant bounded by the coordinate planes and the parabolic cylinders z = 9 1:2 and y = 9 :2. Limits of Integration: " Form:0::a::3. " Fory:D:Zg2.>

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

I need help with these problems, please explain. Thank you. The function at) = 2 + 3x + 483':1 has one local minimum and one local maximum. This function has a local maximum at :0 = :] A company that...

sjeccd.instructure.com 15 Group Quiz C Find The Average Value Of The Following Regions F(.. | Chegg.com Question 11 0.5 pt Find the area of the region specified in polar coordinates. the region...

MATH 251 Spring 2014 Final Exam Simon Fraser University 23 April 2014, 7:00-10:00pm Instructor: Weiran Sun Last Name: First Name: SFU ID: @sfu.ca Signature: Instructions Question Maximum 1. Please do...

1 Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral. The curves and 5 points Question 2 Evaluate the integral. - - 5 points Question 3 Find...

Need Detailed Solution on Paper please clear formatting easy to understand please. for Bonus 3,4,D,E,F and there parts. Everything is mentioned on the paper kindly read it D Bonus 3 Choose one of the...

Course Hero X Content X VA 14.6 Homework - T X Course Hero X H - C webassign.net/web/Student/Assignment-Responses/last?dep=31665156#Q4 Gmail YouTube Maps 4. [-/1 Points] DETAILS LARCALC11 14.6.022....

Need Detailed Explanation of Bonus 3,4, D,F,E and there parts on Paper D Bonus 3 Choose one of the below. An extra page has been left for workspace if you feel you need to use it. 40 pts 1) Let F =...

During the negotiations for NAFTA (North American Free Trade Agreement among the United States, Canada, and Mexico) in the early 1990s, opponents argued that the United States would lose many jobs to...

Discuss about ethnography

9 Discuss an element of risk management with an example.

A hula hoop and solid disc of equal radii are rolled, from rest and without slipping, down an incline plane. Which one will reach the bottom of the inclined plane first? Explain.

Shares bought on 1 January 2010 for 2,500 were sold on 31 December 2014 for 4,400. What was the rate of annual compound interest on the investment?

lf the interest on the investment in Question 45.6 had been compounded every six months, how much interest would have been earned over the four years?

Should you accept an offer of 50,000 for your rights over the next 12 years to the 5,000 annual rent from shop premises you own and have leased to a local company? You could invest the 50,000 at 6%...