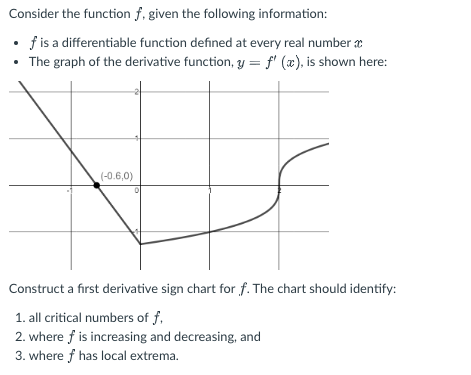
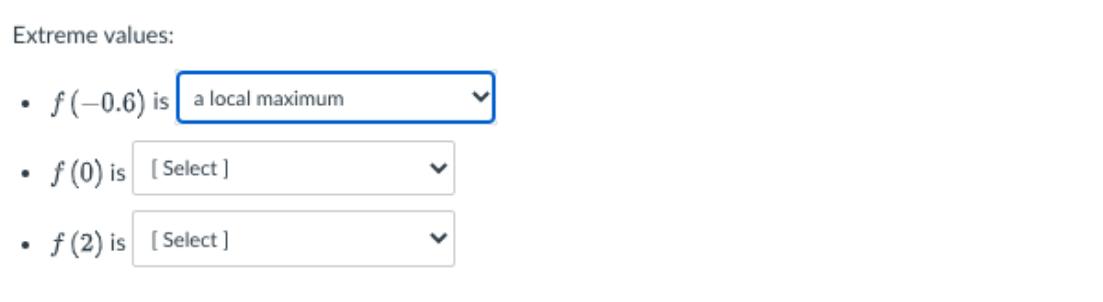
Consider the function f, given the following information: f is a differentiable function defined at every real number The graph of the derivative function, y = f' (a), is shown here: (-0.6,0) Construct a first derivative sign chart for f. The chart should identify: 1. all critical numbers of f, 2. where f is increasing and decreasing, and 3. where f has local extrema. Extreme values: . f(-0.6) is a local maximum f(0) is [Select] f (2) is [Select] Interval (-, -0.6) f f' > 0 conclusion f is increasin First derivative sign chart (-0.6, 0) [Select] f' < 0 f' = 0 f' > 0 (0, 2) f < 0 fis decreasing [Select] [Select] (2,00)