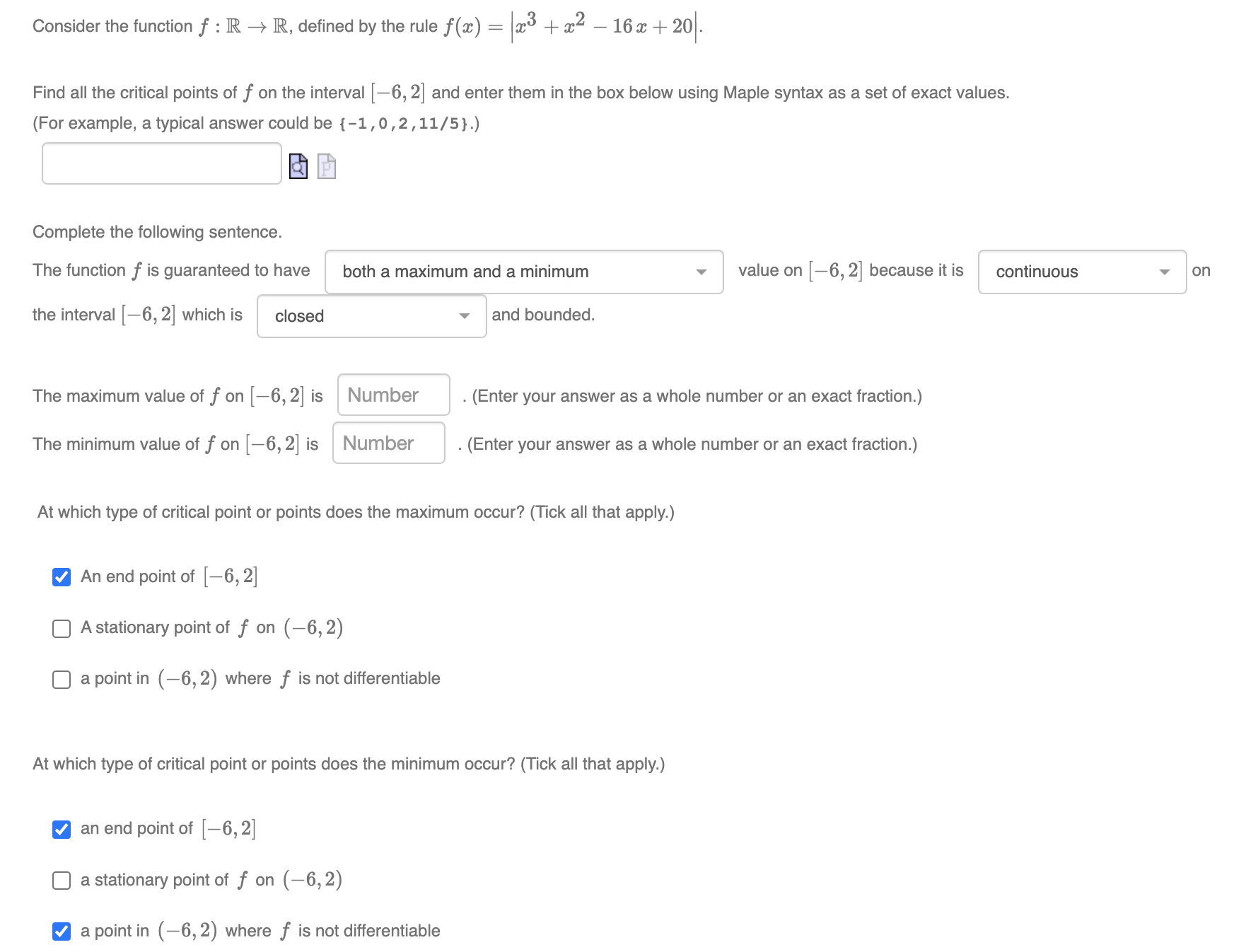
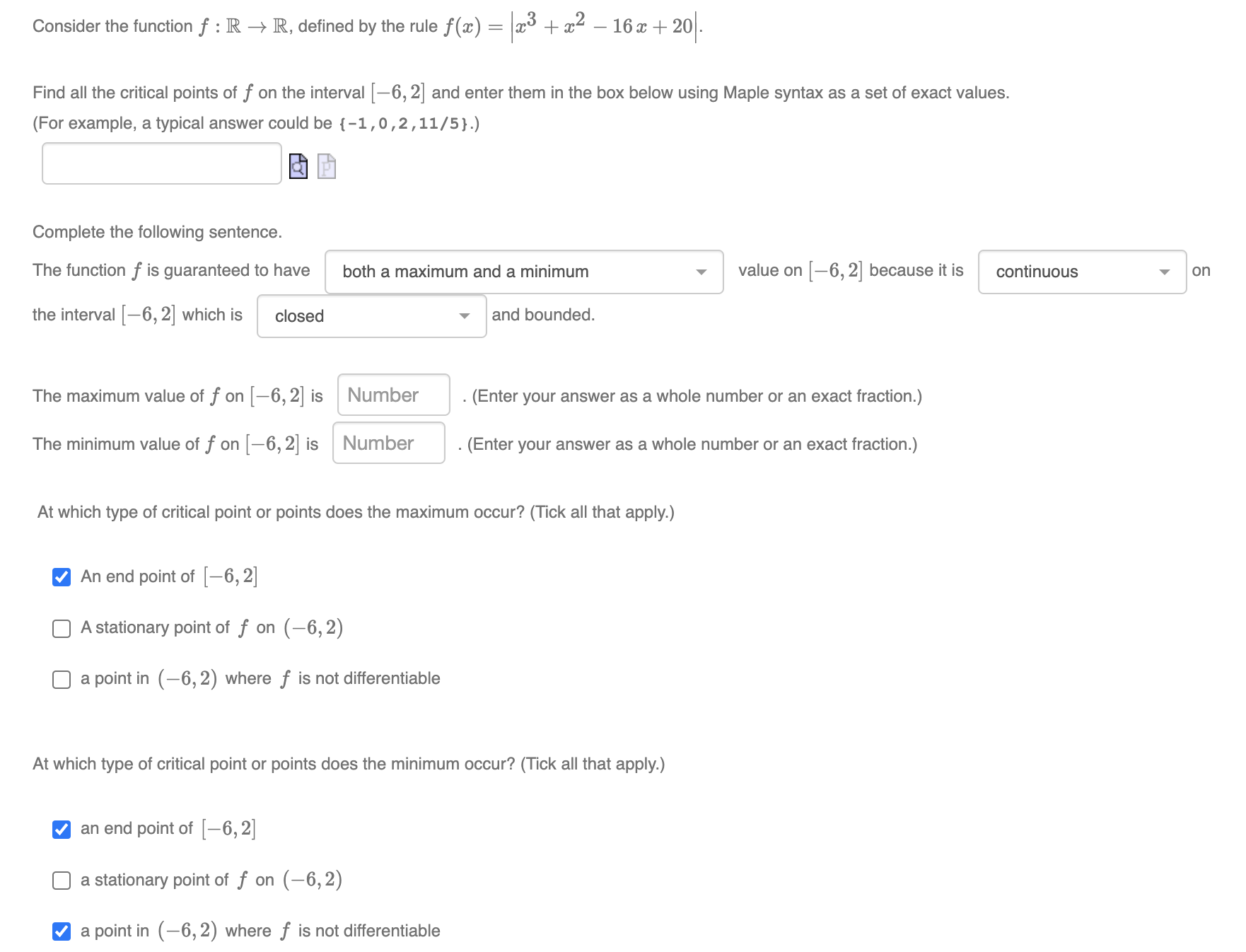
Consider the function f : R - R, defined by the rule f(x) = 23 + x2- 16 a + 20 . Find all the critical points of f on the interval [-6, 2] and enter them in the box below using Maple syntax as a set of exact values. (For example, a typical answer could be {-1 , 0, 2, 11/5}.) Complete the following sentence. The function f is guaranteed to have both a maximum and a minimum value on [-6, 2] because it is continuous on the interval [-6, 2] which is closed and bounded. The maximum value of f on [-6, 2] is Number (Enter your answer as a whole number or an exact fraction.) The minimum value of f on [-6, 2] is Number (Enter your answer as a whole number or an exact fraction.) At which type of critical point or points does the maximum occur? (Tick all that apply.) An end point of [-6, 2] A stationary point of f on (-6, 2) a point in (-6, 2) where f is not differentiable At which type of critical point or points does the minimum occur? (Tick all that apply.) an end point of [-6, 2] a stationary point of f on (-6, 2) a point in (-6, 2) where f is not differentiable