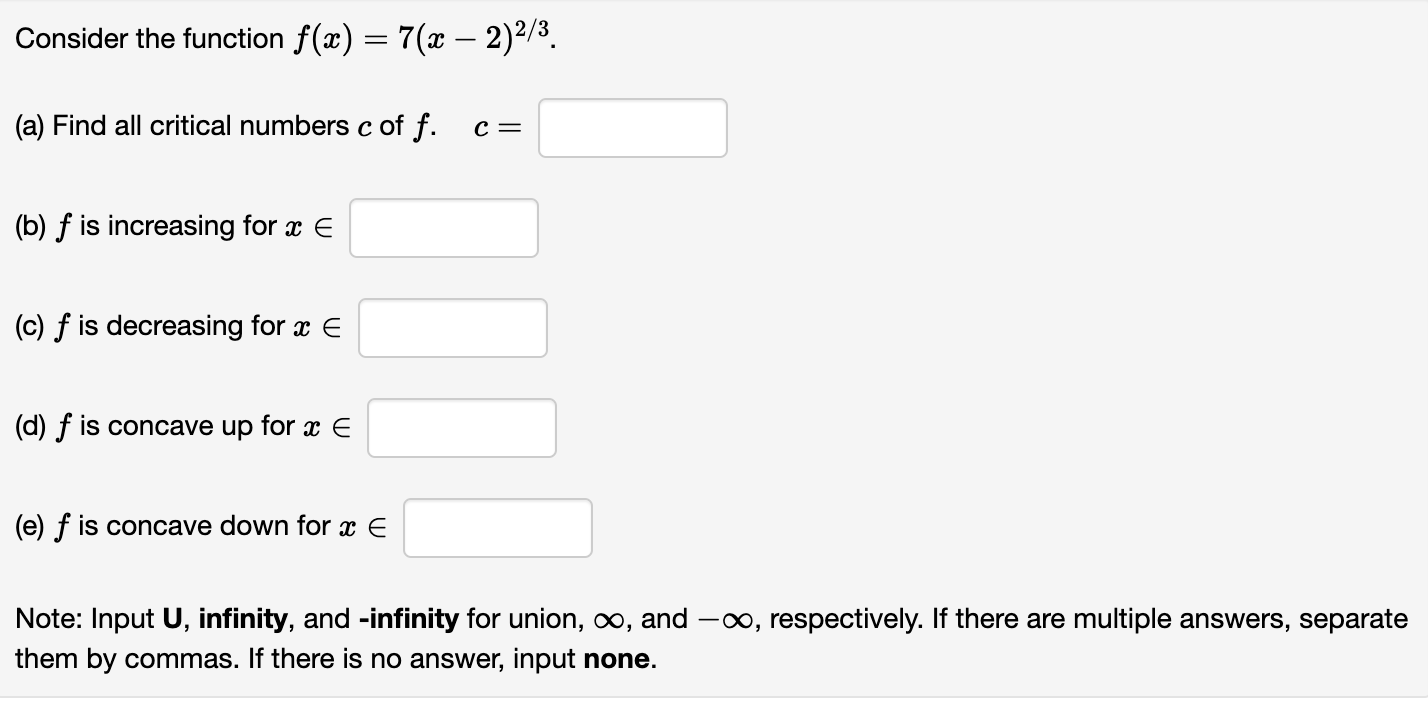
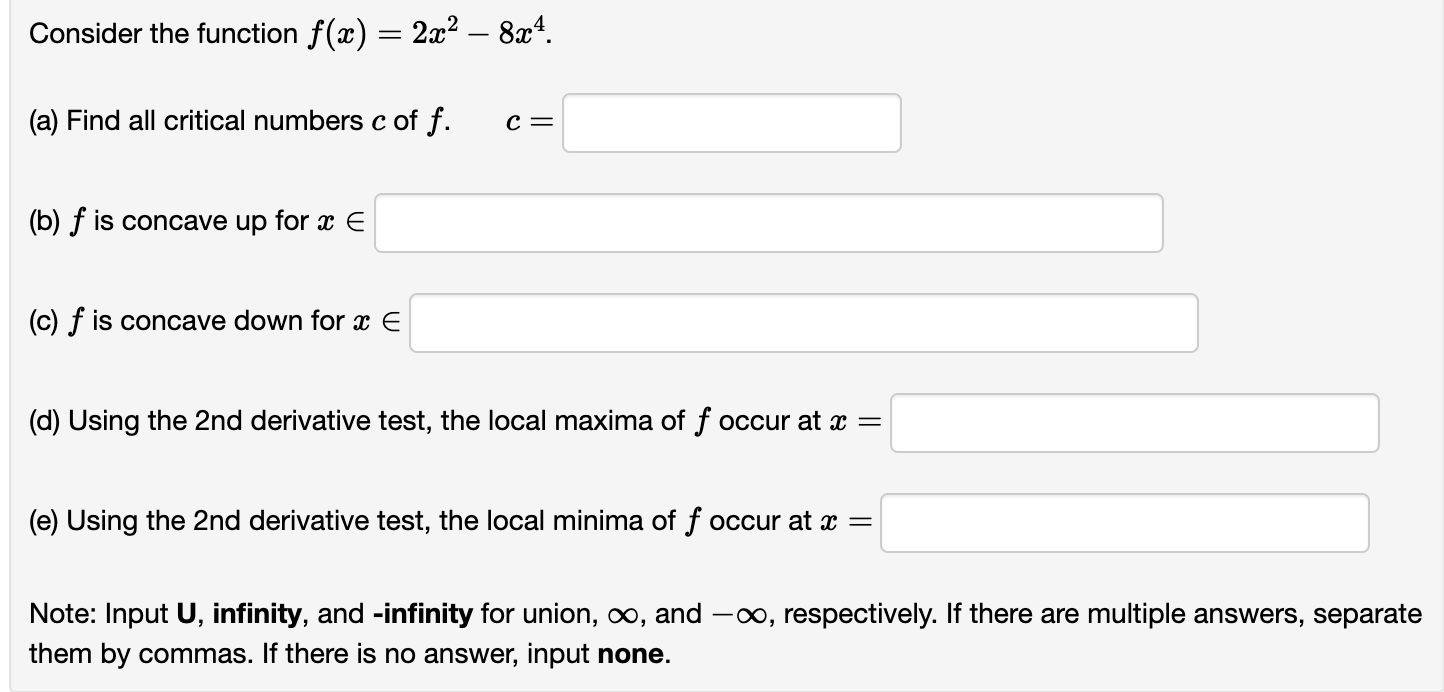
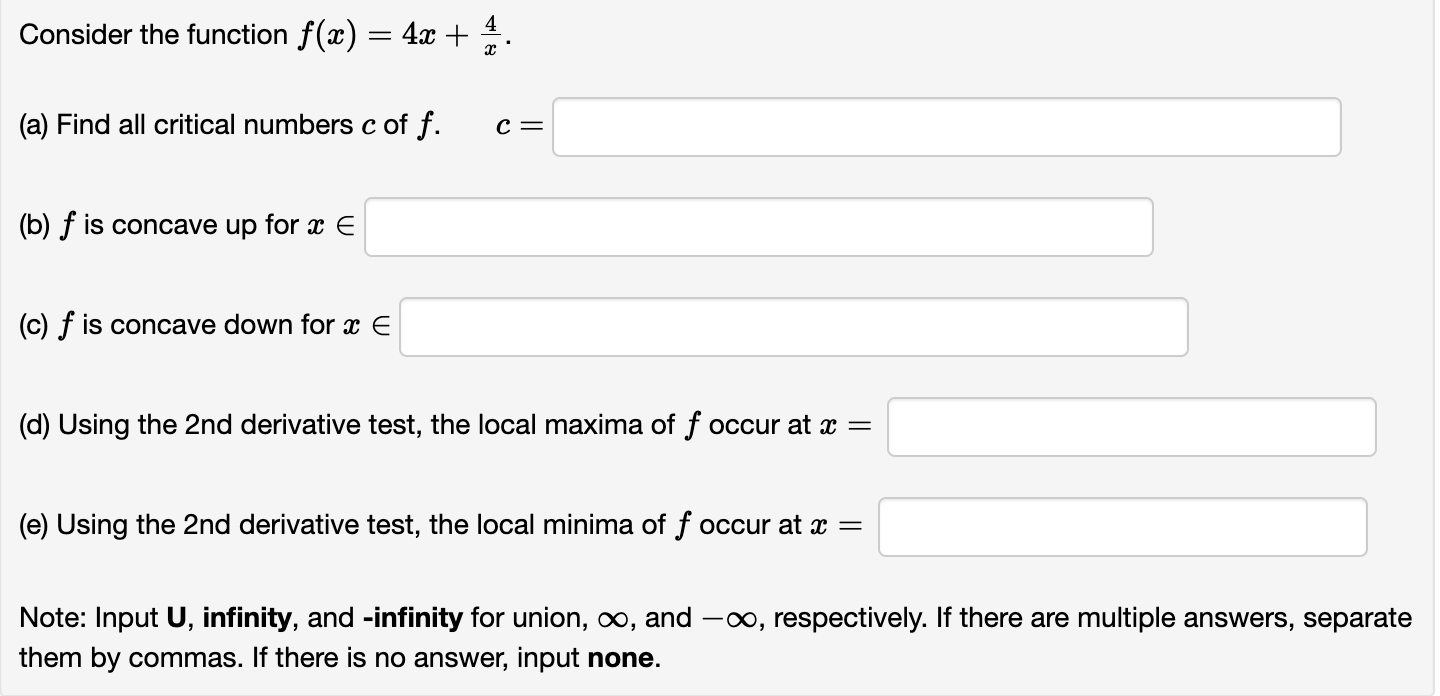
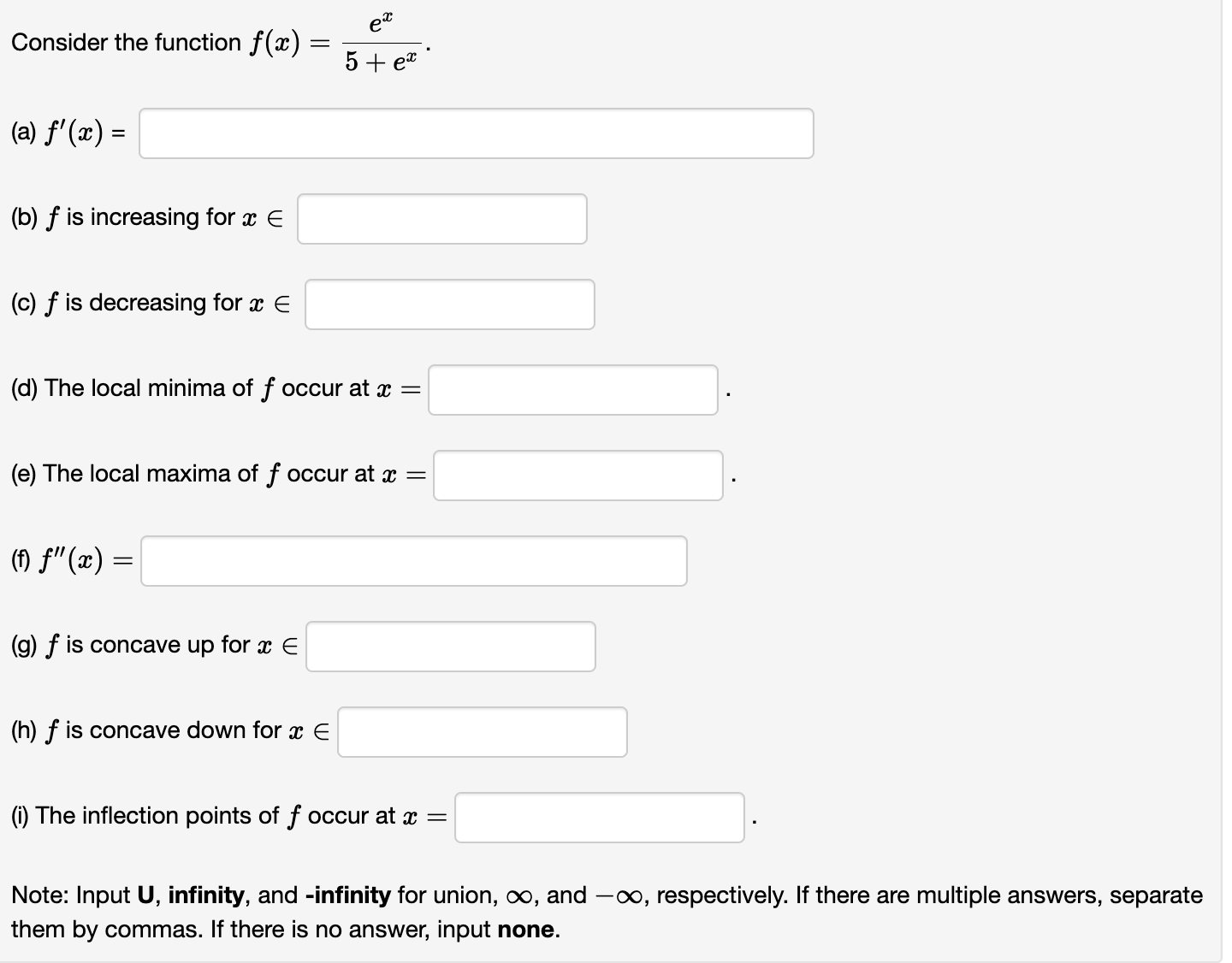
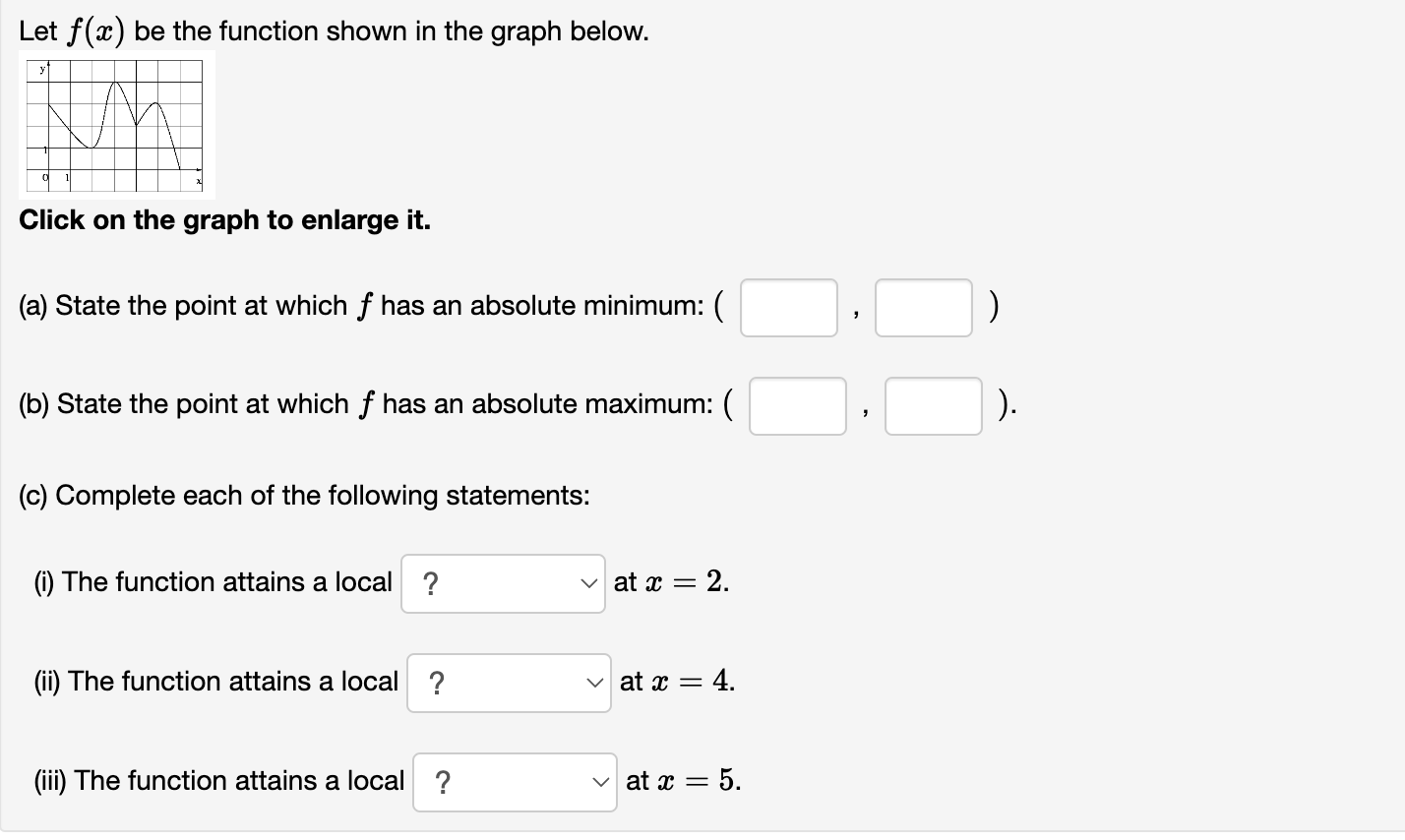
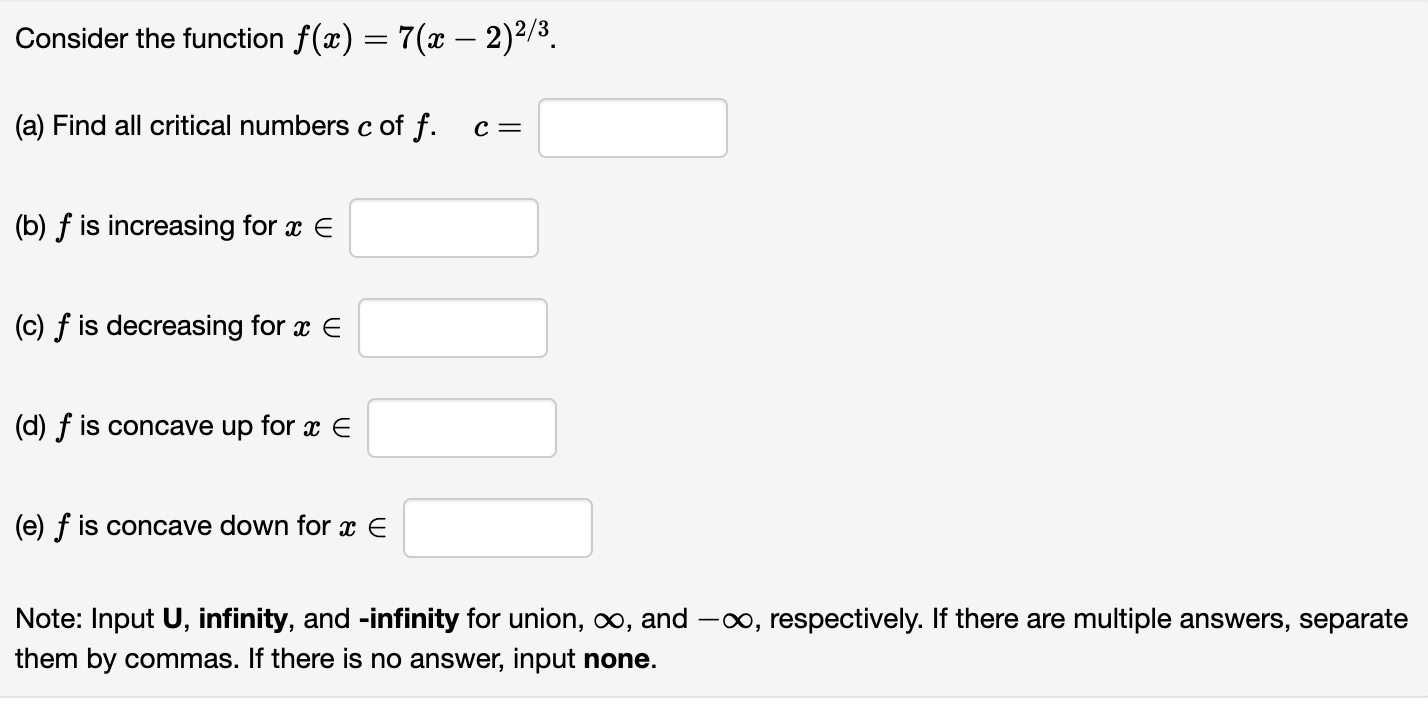
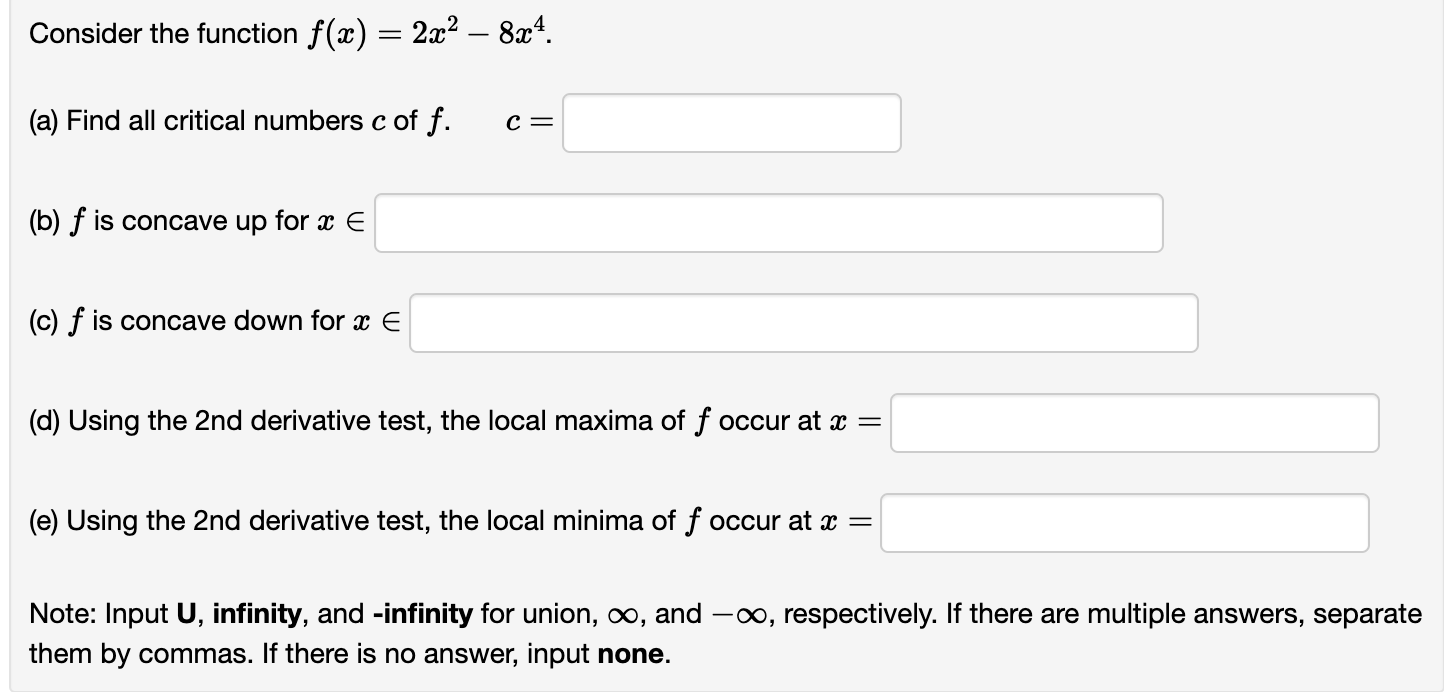
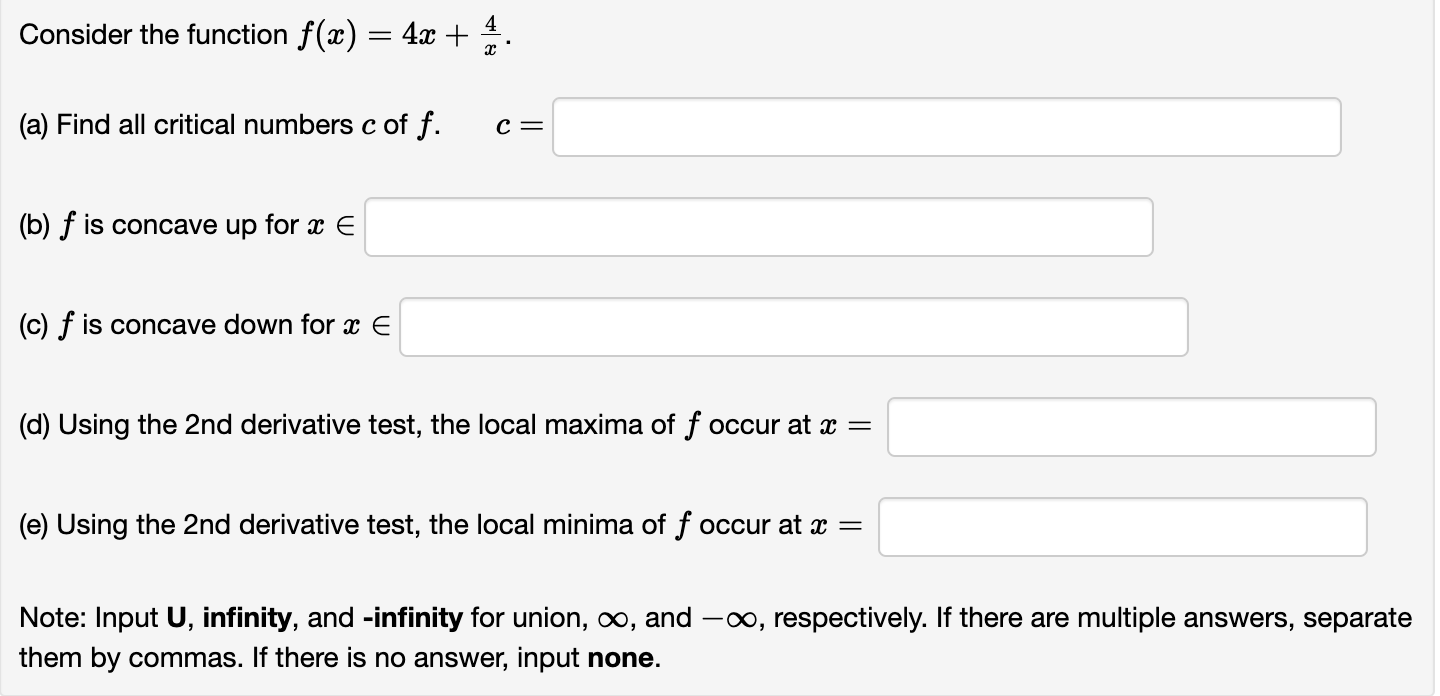
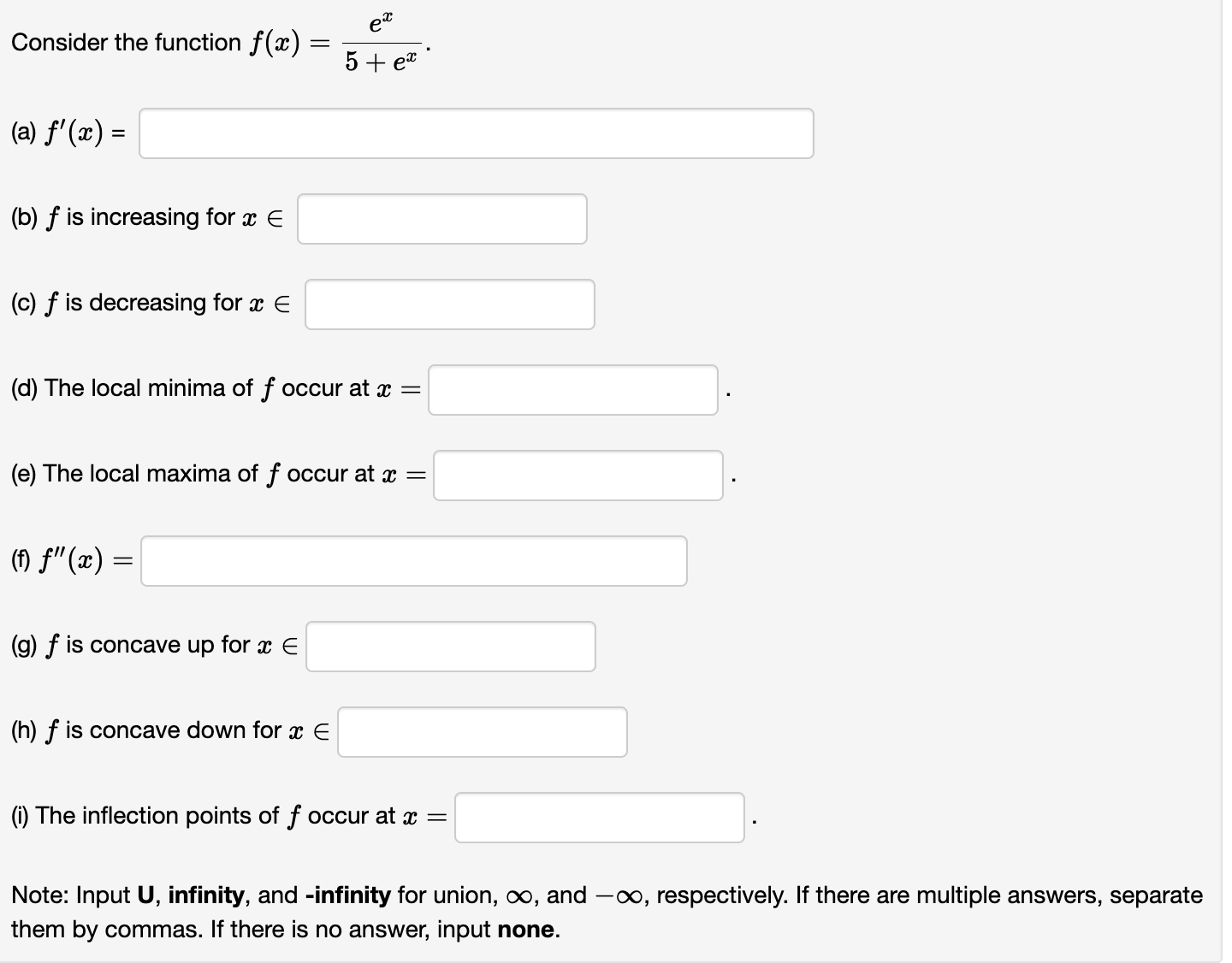
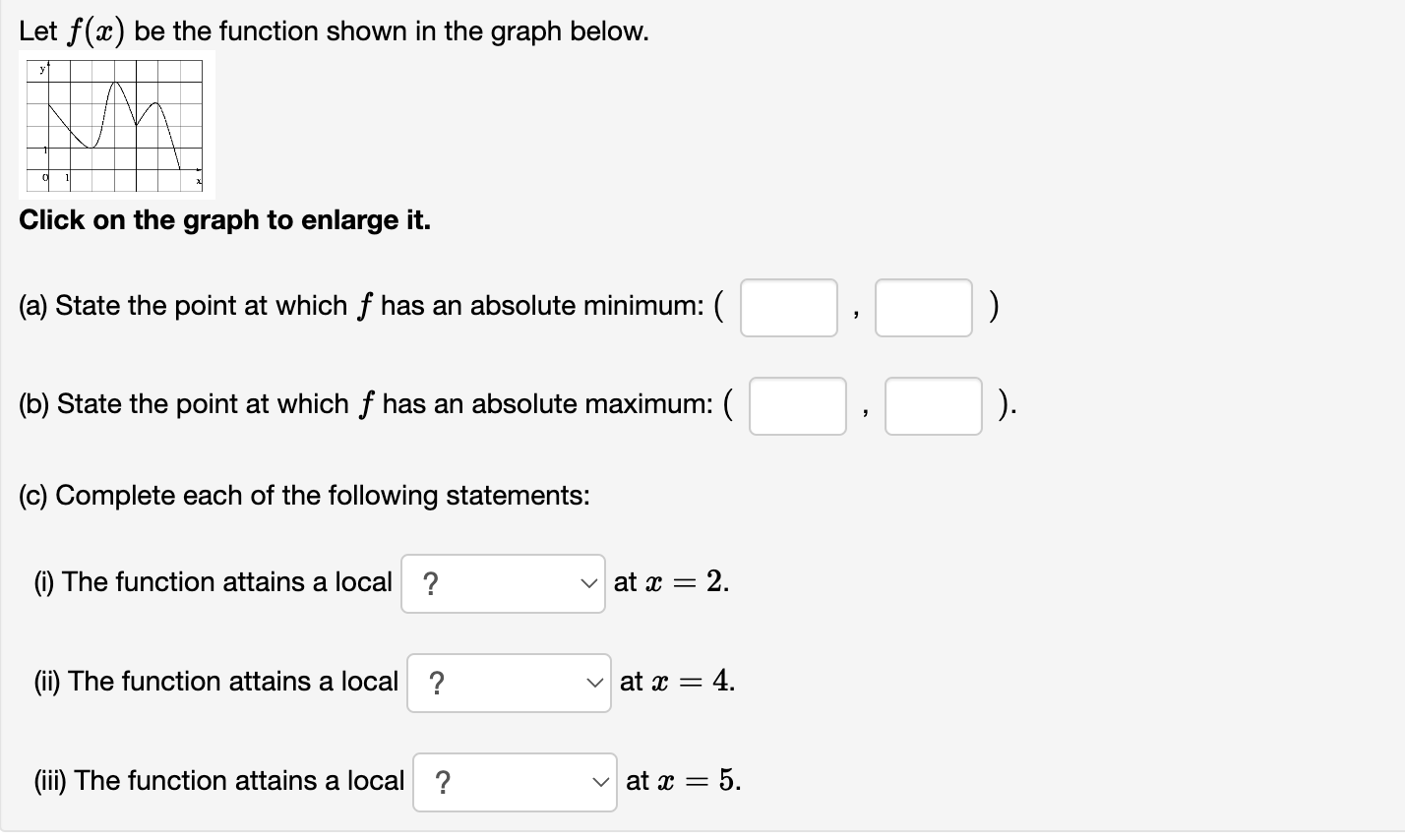
Consider the function x) 2 7(91 2)2/3. (a) Find all critical numbers c off. 0 = (b) f is increasing for m E (c) f is decreasing for a: E (d) f is concave up for a: E (e) f is concave down for a: E Note: Input U, infinity, and -infinity for union, 00, and 00, respectively. If there are multiple answers, separate them by commas. If there is no answer, input none. Consider the function at) : 2:1:2 8334. (a) Find all critical numbers c of f. c = (b) f is concave up for a: E (c) f is concave down for a: E (d) Using the 2nd derivative test, the local maxima of f occur at m : (e) Using the 2nd derivative test, the local minima of f occur at a: 2 Note: Input U, infinity, and -infinity for union, co, and 00, respectively. If there are multiple answers, separate them by commas. If there is no answer, input none. Consider the function ac) : 4:1: + g. (a) Find all critical numbers c of f. c = (b) f is concave up for :1: E (c) f is concave down for m E (d) Using the 2nd derivative test, the local maxima of f occur at :c = (e) Using the 2nd derivative test, the local minima of f occur at a: : Note: Input U, infinity, and -infinity for union, co, and 00, respectively. If there are multiple answers, separate them by commas. If there is no answer, input none. :L' 8 Consider the function f(a:) : 5 + m . e (a) f '(m) = (b) f is increasing for :13 E (c) f is decreasing for :1: E (d) The local minima of f occur at a: = (e) The local maxima of f occur at a: : (f) f"($) : (g) f is concave up for :1: E (h) f is concave down for a: E (i) The inflection points of f occur at m : Note: Input U, infinity, and -infinity for union, co, and 00, respectively. If there are multiple answers, separate them by commas. If there is no answer, input none. Let at) be the function shown in the graph below. 3 \\ . ll \\/\\. A l. . I l \\ 1 Click on the graph to enlarge it. (a) State the point at which f has an absolute minimum: ( (b) State the point at which f has an absolute maximum: ( (0) Complete each of the following statements: (i) The function attains a local ? v at x = 2. (ii) The function attains a local ? v at :17 : 4. (iii) The function attains a local ? v at a: : 5