Question: Consider the functions f ( x ) = x 3 - 6 x 2 + 9 x , and , g ( x ) =
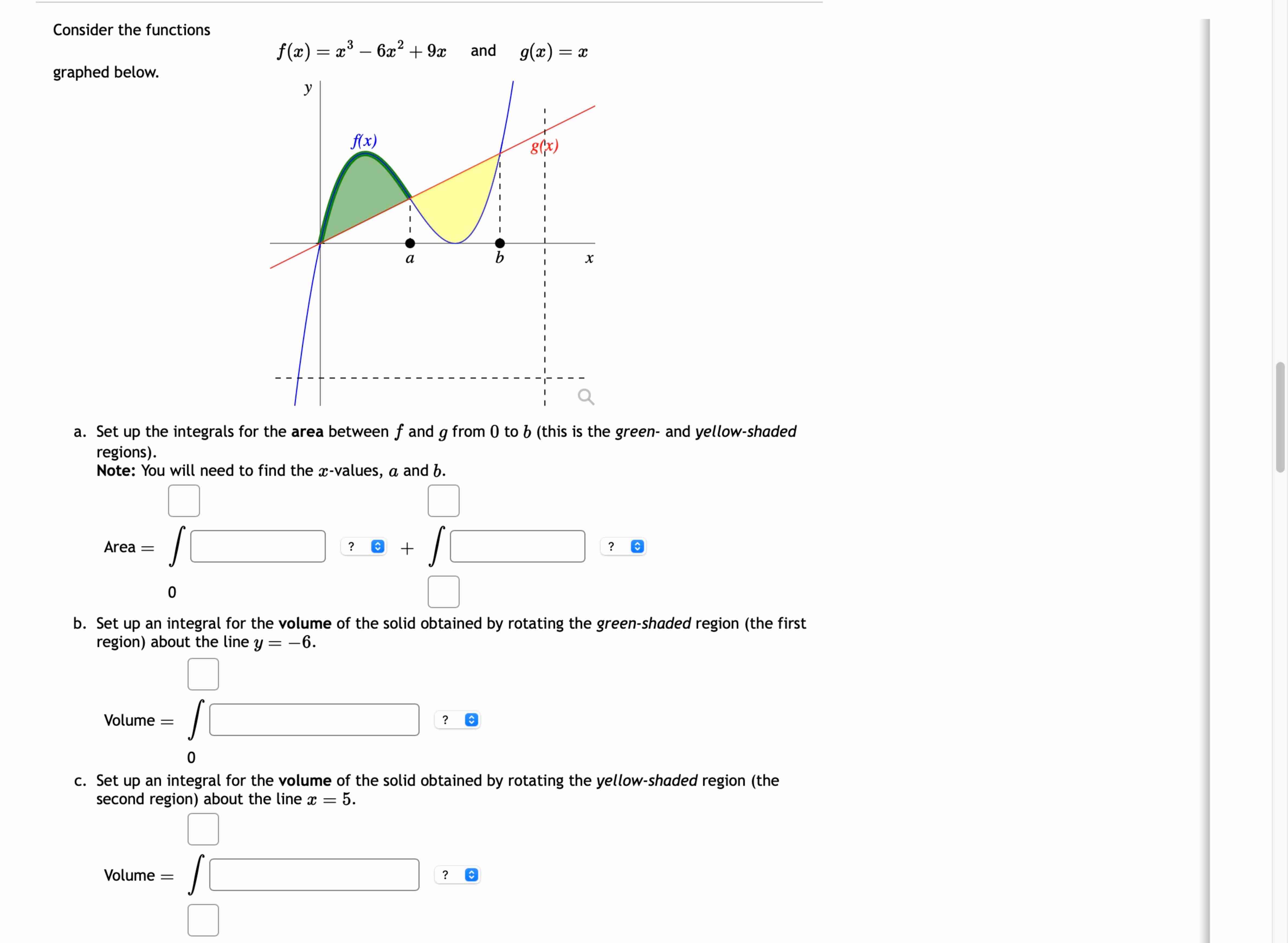
Consider the functions
and
graphed below.
Set the integrals for the area between and from the green and yellowshaded
regions
Note: You will need find the values, a and
Area
Set integral for the volume the solid obtained rotating the greenshaded region first
region about the line
Volume
Set integral for the volume the solid obtained rotating the yellowshaded region
second region about the line
Volume Set integral tor the volume the solid obtained rotating the greenshaded region first region about the line
Volume
Set integral for the volume the solid obtained rotating the yellowshaded region second region about the line
Volume
Set integral for the arc length from
Note: This the same and a from the nrevious three narts.
Arc Length
Finally, set integral for the surface area the solid obtained rotating the shaded region part from a about the axis.
Surface Area
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


