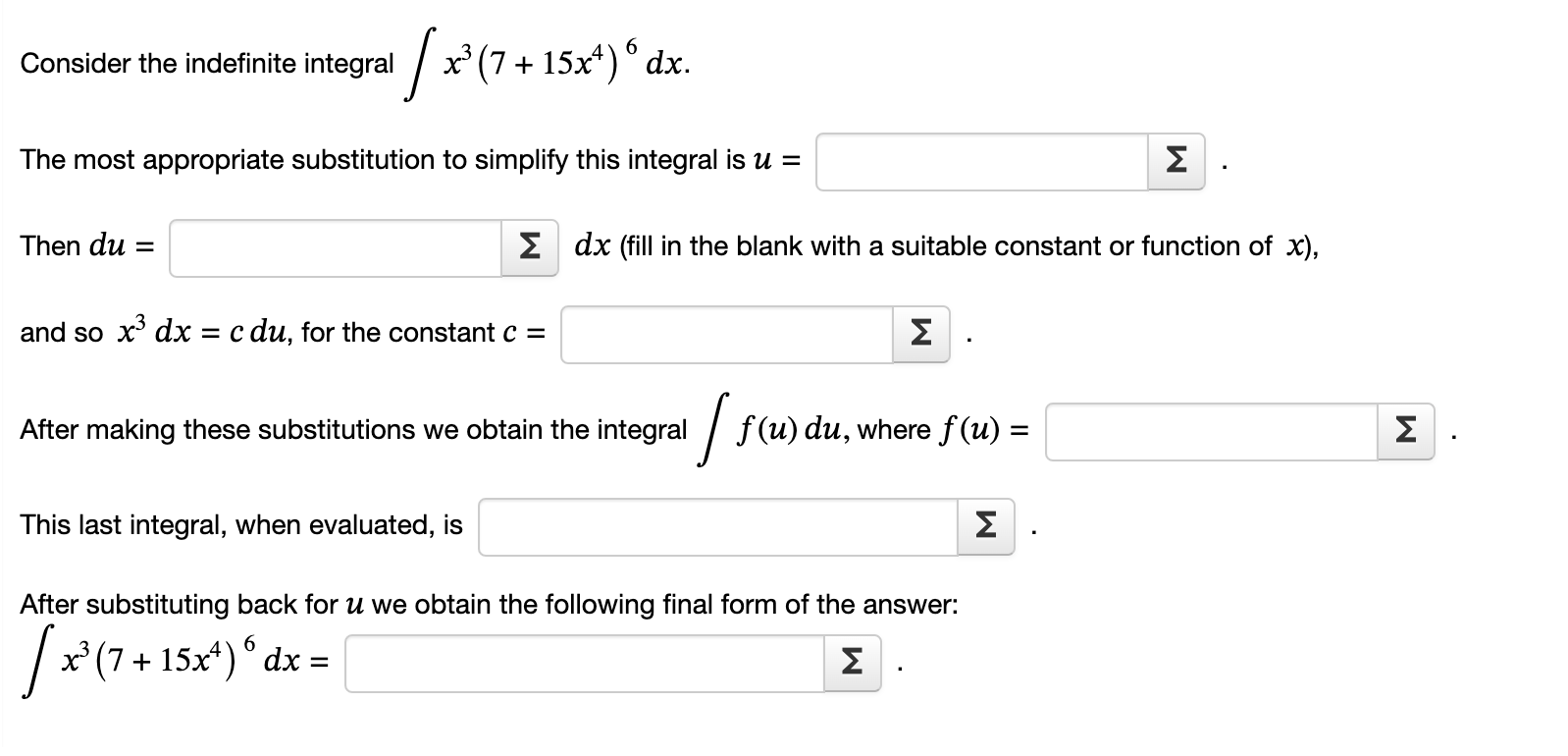
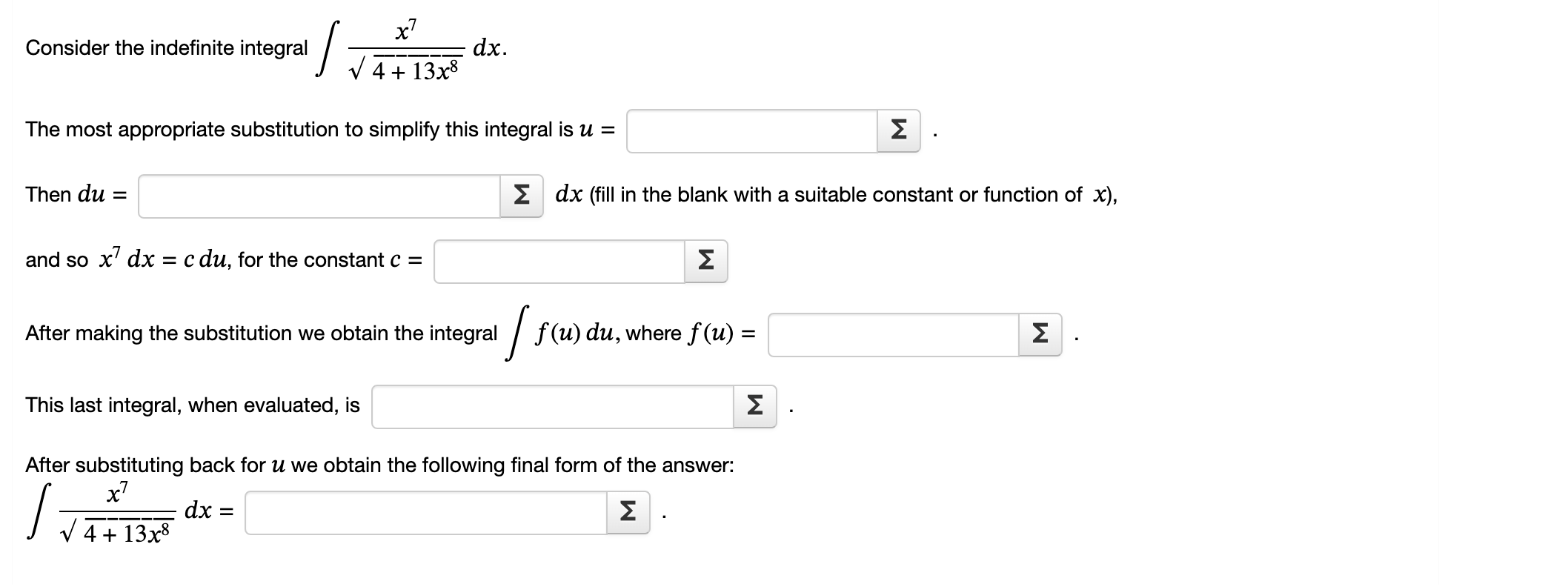
Consider the indefinite integral /x3 (7 + 15x4) 6 dx. The most appropriate substitution to simplify this integral is u = 2 Then du = 2 dx (fill in the blank with a suitable constant or function of x), and so x3 dx = Cdu, for the constant c = 2 After making these substitutions we obtain the integral / f(u) du, where f (u) = This last integral, when evaluated, is 2 After substituting back for u we obtain the following final form of the answer: [x3(7+15x4)6dx= z 7 x Consider the indefinite integral / : dx. 4 + 13x8 The most appropriate substitution to simplify this integral is u = 2 Then du = 2 dx (fill in the blank with a suitable constant or function of x), and so x7 dx = c du, for the constant c = 2 After making the substitution we obtain the integral /f(u) du, where f(u) = Z This last integral, when evaluated, is 2 After substituting back for u we obtain the following final form of the answer: 7 x _____ dx = 2 / \\/ 4+ 13x8 Consider the indefinite integral [60514 (St) sin(5t) dt. The most appropriate substitution to simplify this integral is u = Then (in = 2 dt, so sin(5t) dt = c du, where the constant c = 2 After making the substitution we obtain the integral ff(u) du, where f(u) : This last integral, when evaluated, is 2 After substituting back for u we obtain the following final form of the answer: / cos14(5t) sin(5t) dt =