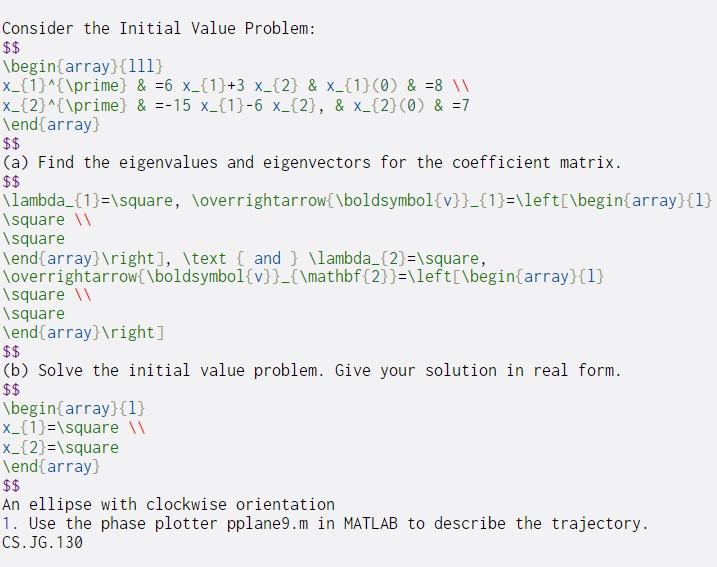
Consider the Initial Value Problem: $$ \begin{array}{111) x_{1}^{\prime & =6 x_{1}+3 x_{2} & x_{1} & =8 x_{2}^{\prime} & =-15 x_{1}-6 x_{2}, & x_{2}(0) & = 7 \end{array) $$ (a) Find the eigenvalues and eigenvectors for the coefficient matrix. $$ \lambda_{1}=\square, "overrightarrow{\boldsymbol{v}}_{1}=\left[\begin{array}{1} \square \square \end{array} ight], \text { and } \lambda_{2}=\square, \overrightarrow{\boldsymbol{v}}_{\mathbf {2}}=\left[\begin{array}{1} \square \square \end{array} ight] $$ (b) Solve the initial value problem. Give your solution in real form. $$ \begin{array}{1} x_{1}=\square x_{2}=\square \end{array} $$ An ellipse with clockwise orientation 1. Use the phase plotter pplane9.m in MATLAB to describe the trajectory. CS. JG.130