Consider the initial value problem

$y^{\text{'}\text{'}}-2y^{\text{'}}-5xy=0,y(0)=-6,y^{\text{'}}(0)=-7$

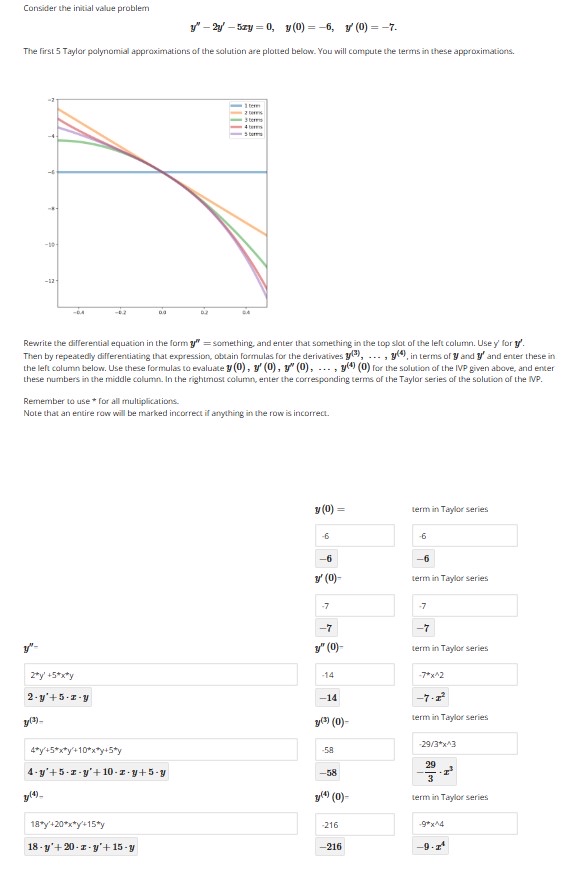
The first $5$ Taylor polynomial approximations of the solution are plotted below. You will compute the terms in these approximations.

Rewrite the differential equation in the form $y^{\text{'}\text{'}}=$ something, and enter that something in the top slot of the left column. Use $y^{\text{'}}$ for $y^{\text{'}}.$ Then by repeatedly differentiating that expression, obtain formulas for the derivatives $y^{(3)},$dots,$y^{(4)},$ in terms of $y$ and $y^{\text{'}}$ and enter these in the left column below. Use these formulas to evaluate $y(0),y^{\text{'}}(0),y^{\text{'}\text{'}}(0),$dots,$y^{(4)}(0)$ for the solution of the IVP given above, and enter these numbers in the middle column. In the rightmast column, enter the corresponding terms of the Taylor series of the solution of the IVP.

Remember to use $*$ for all multiplications.

Note that an entire row will be marked incorrect if anything in the row is incorrect.

$\backslash$table$[[y(0)=,$term in Taylor series$],[y^{\text{'}}(0)-,$term in Taylor series$],[-7,],[y^{\text{'}\text{'}}(0)-,$term in Taylor series$]]$

$2*y^2+5*x*y$

$y^{(3)}-$

$4*y^2+5*x*y^2+10*x*y+5*y$

$y^{(4)}-$

$-14$

$y^{(3)}(0)-$

$-58$

$y^{(4)}(0)-$

$-7*x^2$

term in Taylor series

$-\frac{29}{3}*x^3$

term in Taylor series

$18*y^{\text{'}}+20*x*y^{\text{'}}+15-y$

$-216$

$-9*x^4$

Why its saying wrong? Where I am doing wrong? Can you help me to figure this out?