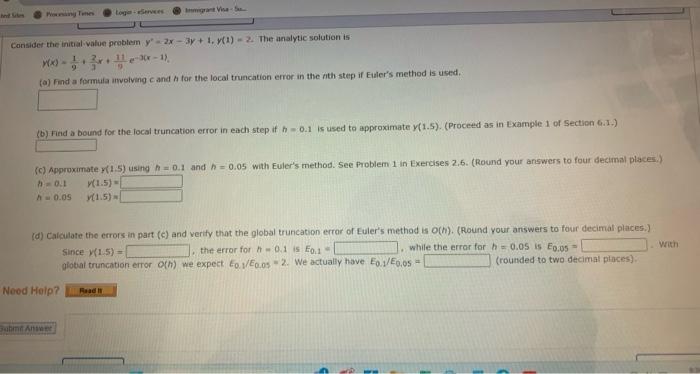
Consider the initial value problem y22x3y+1,y(1)=2. The analytic solution is W(x)=91+72x+911e3(x1). (a) Find a formula unolving c and h for the local truncation error in the ith step if Euler's method is used. (b) Find a bound for the focal truncation error in each step if h=0.1 is used to approximate y(1.5). (Proceed as in Example 1 of Section 6.I.) (c) Approximate (1,5) using h=0.1 and h=0.05 with Euler's method. See Problem 1 in Exercises 2,6 . (Round your answers to four decimal places.) h=0.1h=0.05n(1.5)=y(1.5)= (d) Calculate the errors in part (c) and verify that the global truncation error of Euler's method is o(h) ). (Round your answers to four decimal places.) Since x(1,5)= the error for n=0.1 is E0.1= 1. while the errar for h=0.05 is E0.05= with global truncation error O(h) we expect E0.1/E0,05=2. We actually have E0.1/E0,0,5= (rounded to two decimal places): Neod Heip