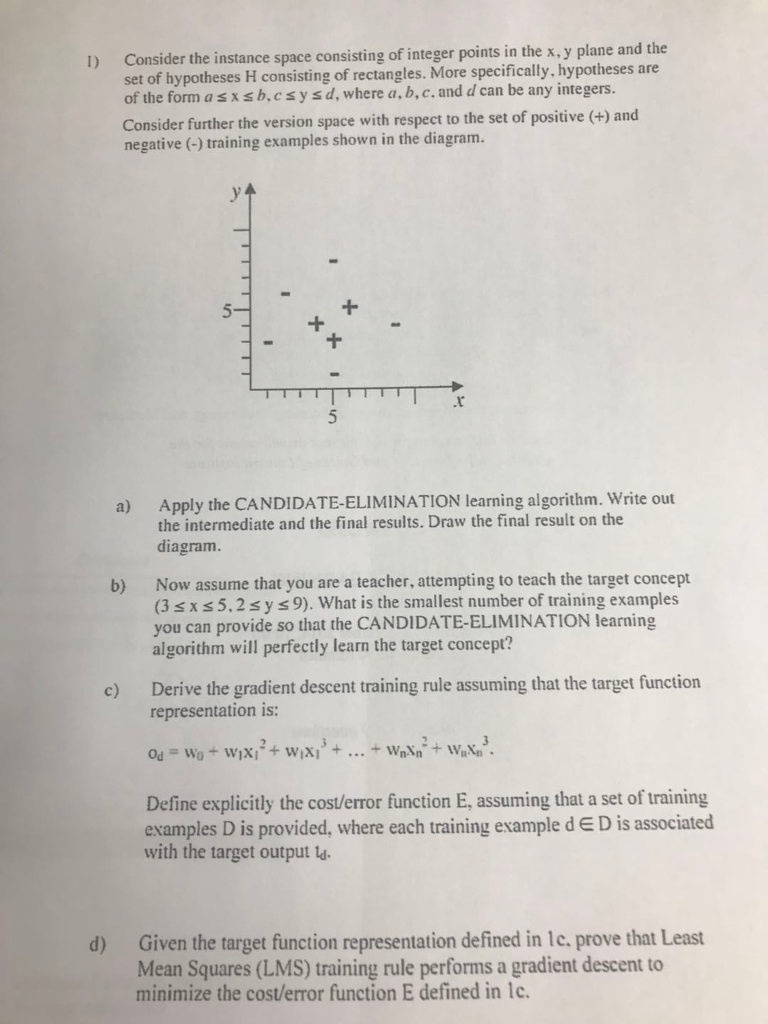
Consider the instance space consisting of integer points in the x, y plane and the set of hypotheses H consisting of rectangles. More specifically, hypotheses are of the form asxsb.csy sd, where a, b,c. and d can be any integers. Consider further the version space with respect to the set of positive (+) and negative training examples shown in the diagram. I) .t Apply the CANDIDATE-ELIMINATION learning algorithm. Write out the intermediate and the final results. Draw the final result on the diagram. a) Now assume that you are a teacher, attempting to teach the target concept (3 sxs5.2sy s9). What is the smallest number of training examples you can provide so that the CANDIDATE-ELIMINATION learning algorithm will perfectly learn the target concept? b) Derive the gradient descent training rule assuming that the target function representation is: c) Define explicitly the cost/error function E, assuming that a set of training examples D is provided, where each training example d E D is associated with the target output ls Given the target function representation defined in 1c. prove that Least Mean Squares (LMS) training rule performs a gradient descent to minimize the cost/error function E defined in 1c. d) Consider the instance space consisting of integer points in the x, y plane and the set of hypotheses H consisting of rectangles. More specifically, hypotheses are of the form asxsb.csy sd, where a, b,c. and d can be any integers. Consider further the version space with respect to the set of positive (+) and negative training examples shown in the diagram. I) .t Apply the CANDIDATE-ELIMINATION learning algorithm. Write out the intermediate and the final results. Draw the final result on the diagram. a) Now assume that you are a teacher, attempting to teach the target concept (3 sxs5.2sy s9). What is the smallest number of training examples you can provide so that the CANDIDATE-ELIMINATION learning algorithm will perfectly learn the target concept? b) Derive the gradient descent training rule assuming that the target function representation is: c) Define explicitly the cost/error function E, assuming that a set of training examples D is provided, where each training example d E D is associated with the target output ls Given the target function representation defined in 1c. prove that Least Mean Squares (LMS) training rule performs a gradient descent to minimize the cost/error function E defined in 1c. d)