Consider the k-Nearest Neighbor (k-NN) classifier for 2 classes ₁ and ₂. Suppose that we have N training samples.

(a) For a 2-NN classifier, we have the following tie-breaking rule: if the two nearest neighbors have opposing labels, we discard the sample, and no error is recorded. Show that as N , the conditional error of the 2-NN classier, P_2-NN(error|x), is half of that of the 1-NN classifier.

(b) Now consider the alternative tie-breaking rule: if the two nearest neighbors have opposing labels, we flip a fair coin and assign ₁ for heads and ₂ for tails. As N , find the conditional error of the 2-NN classifier, P_2-NN(error|x).

(c) If P(z S_e) > 0 for a hypersphere S_e of radius e > 0, then for any of m k nearest neighbors of a point x, we have: x_(m) ^a.s. x, as N .

(d) For the k-NN classifier, with odd k, show that as N , P_k-NN(error|x)

converges almost surely to:

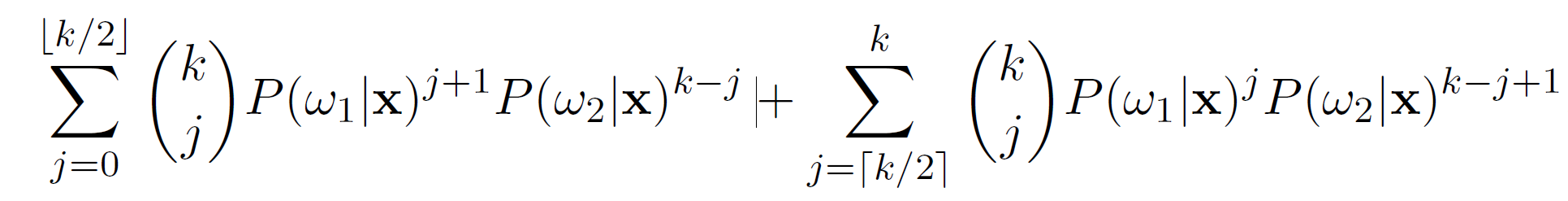
\f