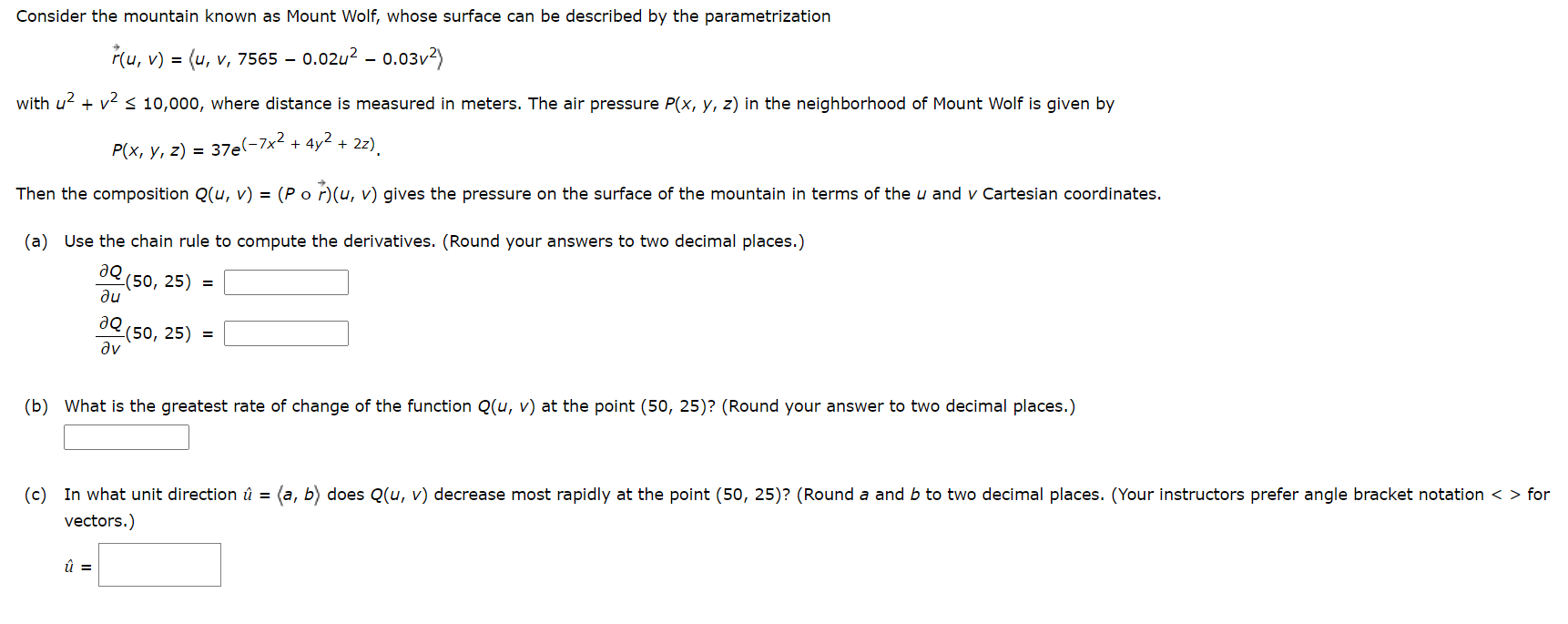
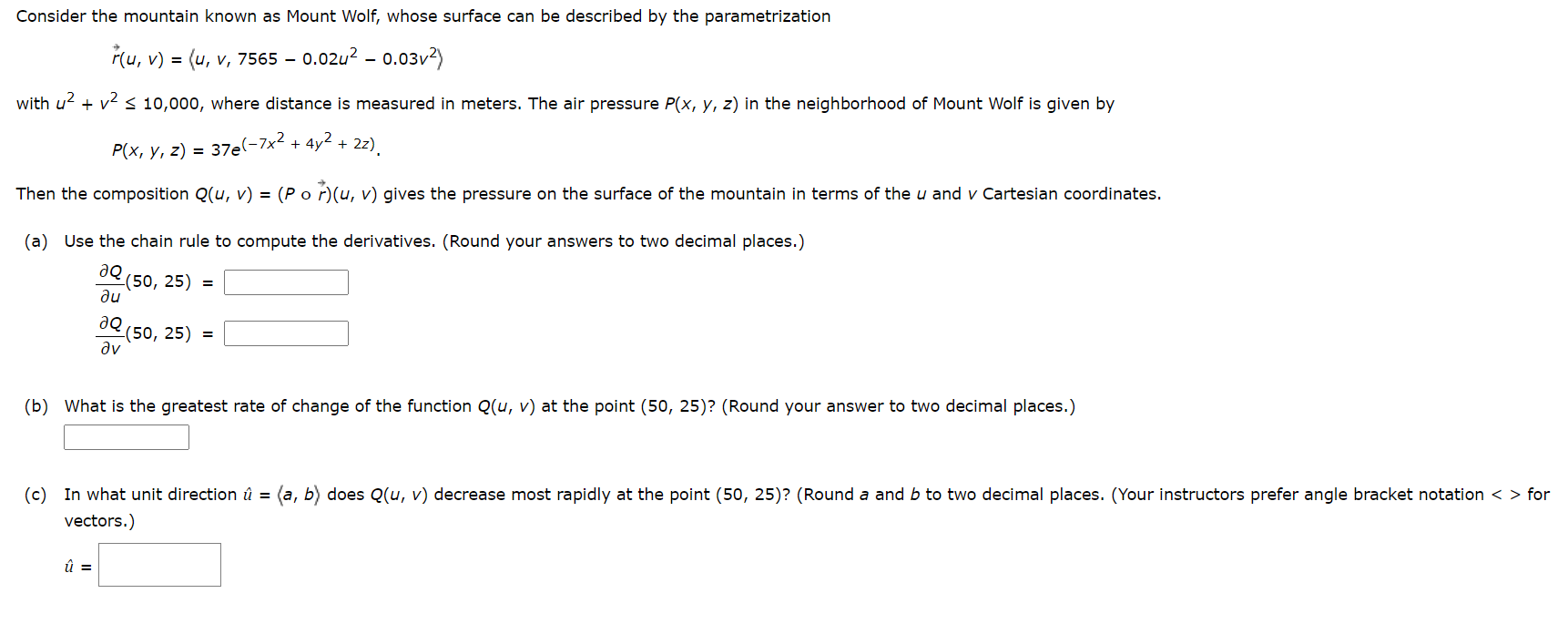
Consider the mountain known as Mount Wolf, whose surface can be described by the parametrization F(u, v) = (u, v, 7565 0.02u2 0.03v2) With U2 + v2 5 10,000, where distance is measured in meters. The air pressure P(x, y, z) in the neighborhood of Mount Wolf is given by (7x2 + 4y2 + 22) P(X, y, z) = 376 . Then the composition Q(u, v) = (P o qu, v) gives the pressure on the surface of the mountain in terms of the u and v Cartesian coordinates. (a) Use the chain rule to compute the derivatives. (Round your answers to two decimal places.) 33.50. 25) = |:| u av |:| o; :0 U1 0 N u1 V II (b) What is the greatest rate of change of the function Q(u, v) at the point (50, 25)? (Round your answer to two decimal places.) S (c) In what unit direction 1': = (a, b) does Q(u, v) decrease most rapidly at the point (50, 25)? (Round 5 and b to two decimal places. (Your instructors prefer angle bracket notation for vectors.) Ll