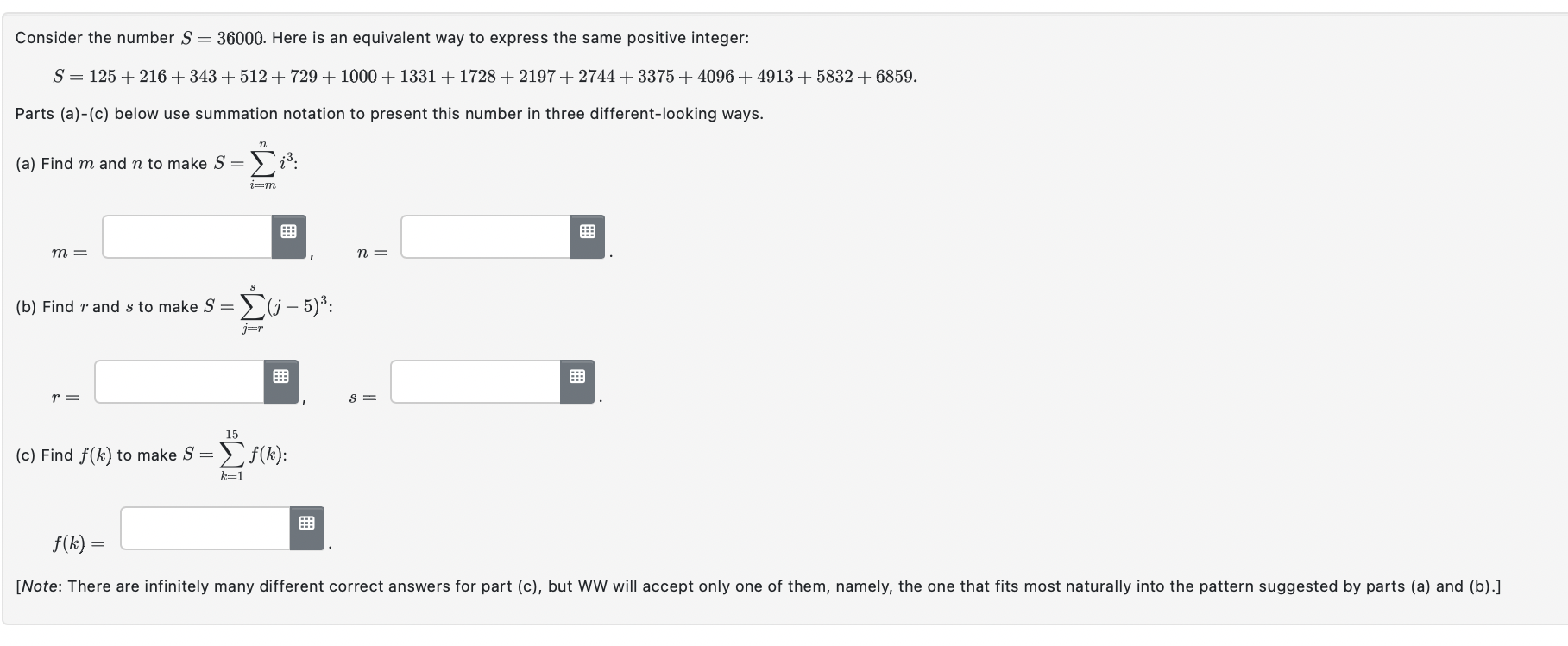
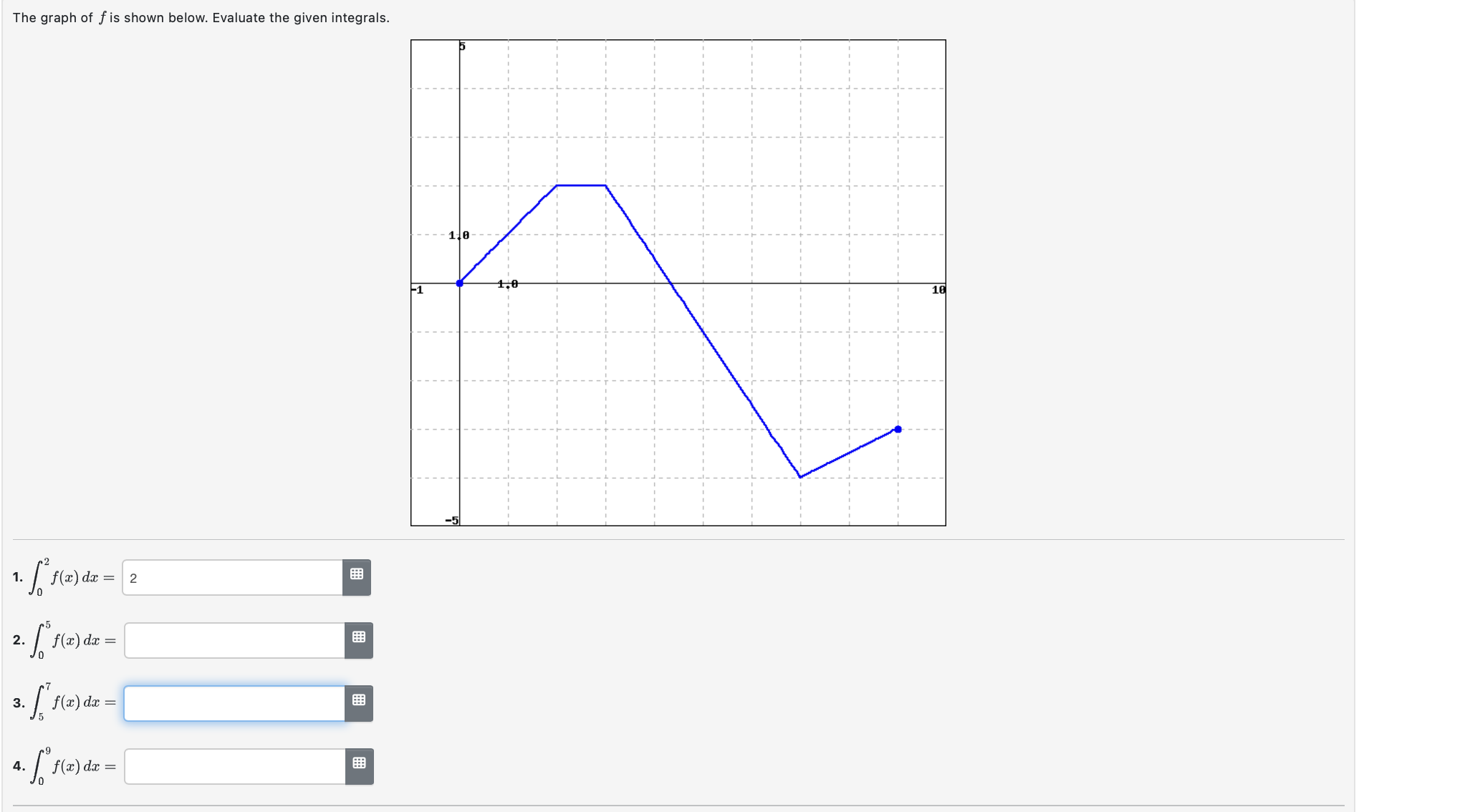
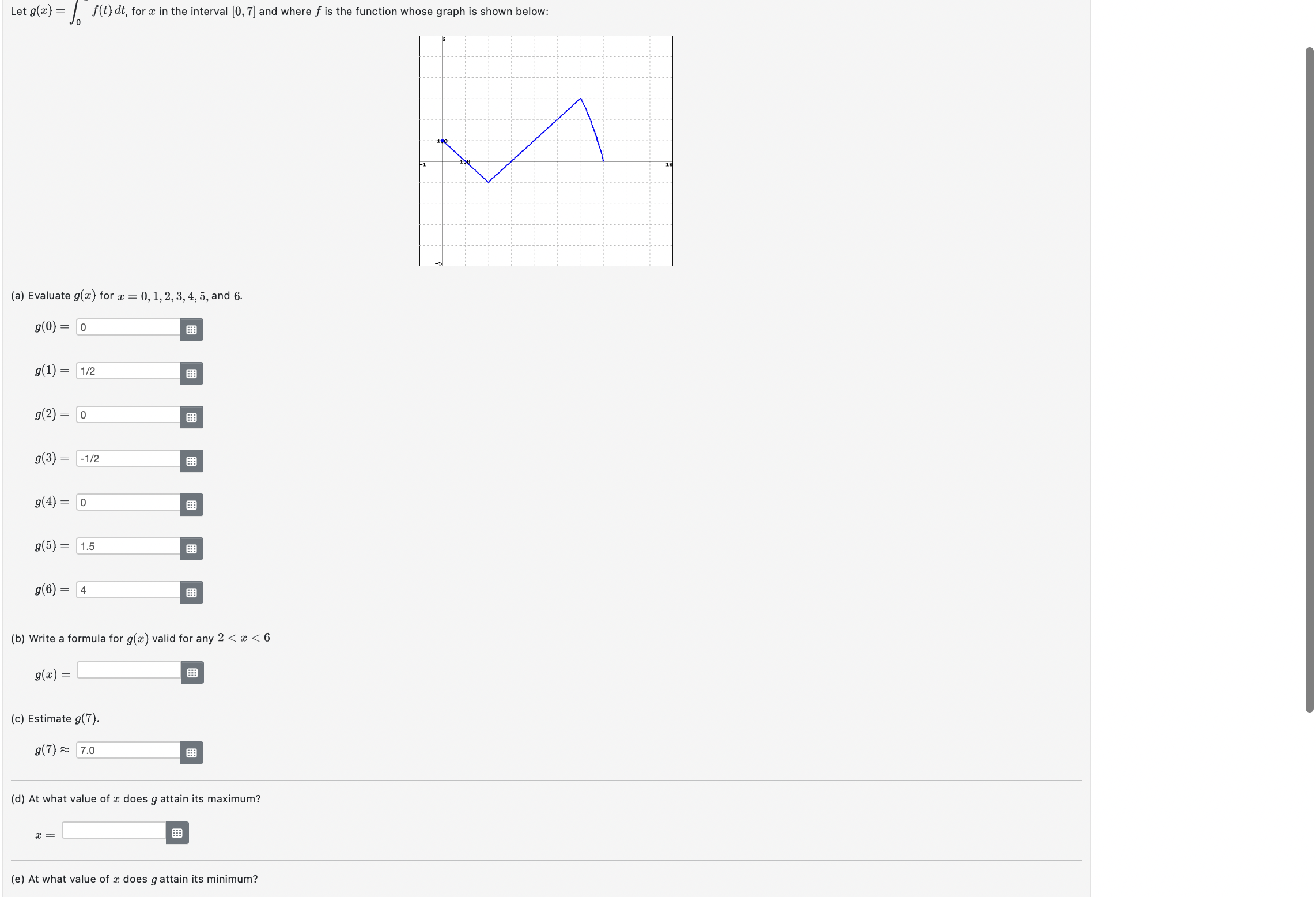
Consider the number S = 36000. Here is an equivalent way to express the same positive integer: S = 125+216 +343 +512+729 +1000 + 1331 +1728 +2197+2744+3375 +4096 +4913 + 5832 +6859. Parts (a)-(c) below use summation notation to present this number in three different-looking ways. (a) Find m and n to make S = : m = r = n i=m 8 (b) Find r and s to make S = (j - 5): j=r k=1 15 (c) Find f(k) to make S = f(k): n = S= f(k)= [Note: There are infinitely many different correct answers for part (c), but WW will accept only one of them, namely, the one that fits most naturally into the pattern suggested by parts (a) and (b).] The graph of f is shown below. Evaluate the given integrals. 1. [* (2) dx = [2 f(x) 2. [ f(2) dax = [ 3. [ f(x) dx = 4. [." f(2) dx = [ -1 0 16 Given the four points in the plane A = (1, 7), B = (2, 8), C = (4, 1), and D = (9,6), the graph of the function f(x) consists of the three line segments AB, BC, and CD. Evaluate the integral below. [ f( f(x) dx: Let g(x) = f(t) dt, for x in the interval [0,7] and where is the function whose graph is shown below: (a) Evaluate g(x) for x = 0, 1, 2, 3, 4, 5, and 6. g(0) 0 g(1) = = g(2) = g(3) g(4) = = 0 g(5) = 1/2 -1/2 0 x = 1.5 g(6) = 4 (b) Write a formula for g(x) valid for any 2 < x < 6 g(x) = (c) Estimate g(7). g(7) 7.0 (d) At what value of a does g attain its maximum? (e) At what value of x does gattain its minimum?