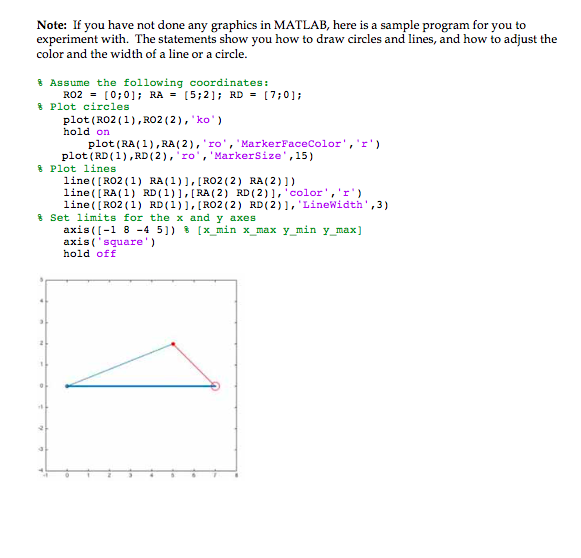
Consider the offset slider-crank mechanism shown. Develop a MATLAB program to compute the unknown position, velocity, and acceleration variables. Use the following constant lengths: L_2 = 0.12 units for the crank, L_3 = 0.26 units for the connecting rod, and a = 0.04 units for the offset. (a) For theta_2 = 30 degree, compute the values of theta_3 and R_ (b) For the known position values from (a), assume omega_2 = 1.0 rad/sec. Compute the values of omega_3 and R_ (c) For the known position and velocity values from. (a) and (b), assume alpha_2 = 0 rad/sec^2. Compute the values of alpha_3 and R_ (d) Repeat (a)-(c) for theta_2 = 240 degree. Report all the results. Add a graphical output to your program to show the position vectors in the vector loop equation. Assume an x-y reference frame with its origin at O_2. Determine the coordinates of O_2, Q, A, and B. (a) Draw circles at O_2, Q, A, and B. (b) Draw lines between O_2 and A, A and B, and B and Q. Include a hardcopy of your program with a snapshot of the displayed graphics with your assignment. % Assume the following coordinates: RO2 = (0: 0): RA = [5: 2]: RD = [7: 0]: % Plot circles plot (RO2(1), RO2(2), "ko") hold on plot (RA(1), RA(2), 'ro' , 'MarkerFaceColor' , 'r') plot(RD(1), RD(1), 'ro', 'MArkerSize', 15) % Plot lines line([RO2(1) RA(1)], [RO2(2) RA(2)]) line([RA(1) RD(1)], [RA(2) RD(2)], 'color' , 'r') line ([RO2(1) RD(1)], [RO2 (2) RD(2)], 'LineWidth', 3) % Set limits for the x and y axes axis([-1 8 -4 5]) % [x_min x_max y_min y_max] axis('square') hold off Consider the offset slider-crank mechanism shown. Develop a MATLAB program to compute the unknown position, velocity, and acceleration variables. Use the following constant lengths: L_2 = 0.12 units for the crank, L_3 = 0.26 units for the connecting rod, and a = 0.04 units for the offset. (a) For theta_2 = 30 degree, compute the values of theta_3 and R_ (b) For the known position values from (a), assume omega_2 = 1.0 rad/sec. Compute the values of omega_3 and R_ (c) For the known position and velocity values from. (a) and (b), assume alpha_2 = 0 rad/sec^2. Compute the values of alpha_3 and R_ (d) Repeat (a)-(c) for theta_2 = 240 degree. Report all the results. Add a graphical output to your program to show the position vectors in the vector loop equation. Assume an x-y reference frame with its origin at O_2. Determine the coordinates of O_2, Q, A, and B. (a) Draw circles at O_2, Q, A, and B. (b) Draw lines between O_2 and A, A and B, and B and Q. Include a hardcopy of your program with a snapshot of the displayed graphics with your assignment. % Assume the following coordinates: RO2 = (0: 0): RA = [5: 2]: RD = [7: 0]: % Plot circles plot (RO2(1), RO2(2), "ko") hold on plot (RA(1), RA(2), 'ro' , 'MarkerFaceColor' , 'r') plot(RD(1), RD(1), 'ro', 'MArkerSize', 15) % Plot lines line([RO2(1) RA(1)], [RO2(2) RA(2)]) line([RA(1) RD(1)], [RA(2) RD(2)], 'color' , 'r') line ([RO2(1) RD(1)], [RO2 (2) RD(2)], 'LineWidth', 3) % Set limits for the x and y axes axis([-1 8 -4 5]) % [x_min x_max y_min y_max] axis('square') hold off