Consider the (partial) branch and bound tree developed for the following integer programming model. (IP) Minz=6x1+7x2+4x3)

subject to 4x1+6x2+9x3>=45

8x1+6x2+3x3>=46

x1,x2,x3>=0

a.)provide the best lower bound for the optimal value of the IP.

b.)provide the best upper bound for the optimal value of the IP.

c.)Is it possible to find an optimal solution by processing node 2 ? why?

d.) consider nodes 3 and nodes 4. What can you say about these nodes. Explain.

e.)Show that any feasible solutions of the IP satisfies following inequality: x_1+x_2+x_3 >= 8

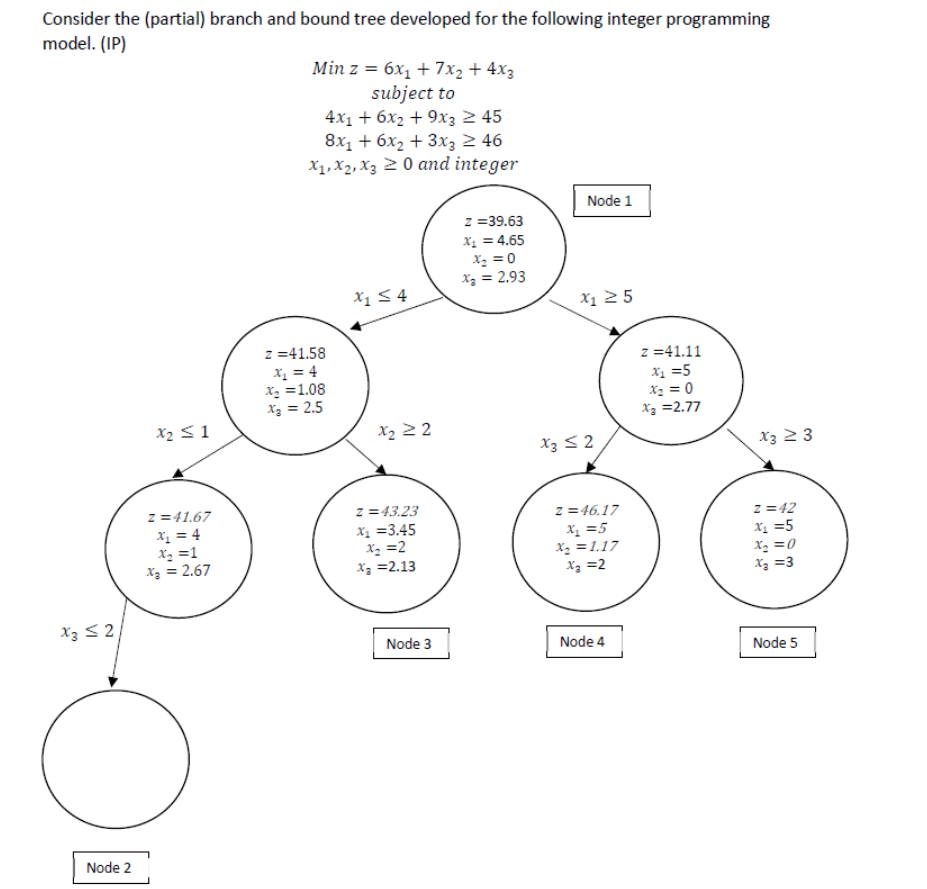
Consider the (partial) branch and bound tree developed for the following integer programming model. (IP) Minz=6x1+7x2+4x2