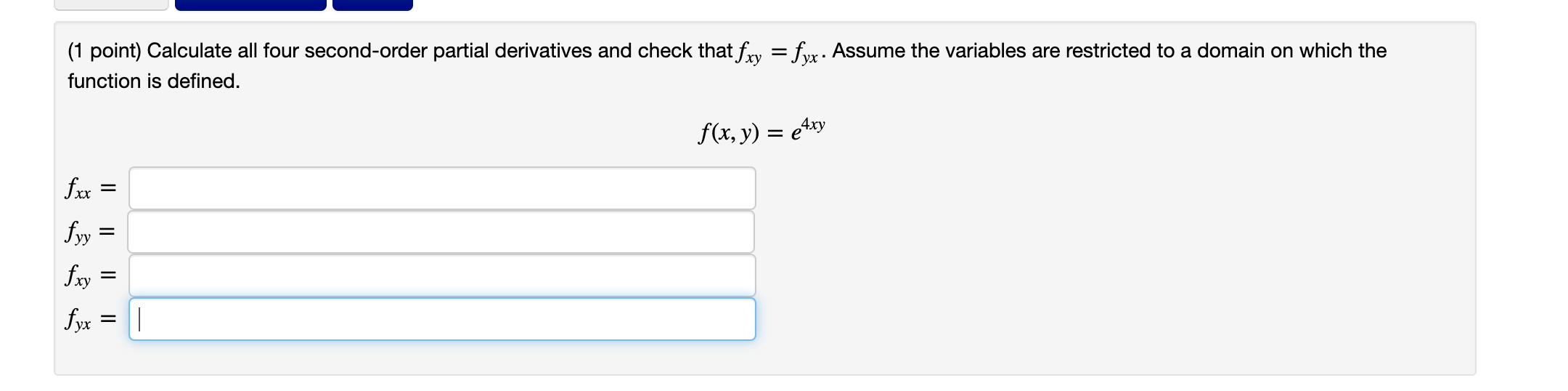
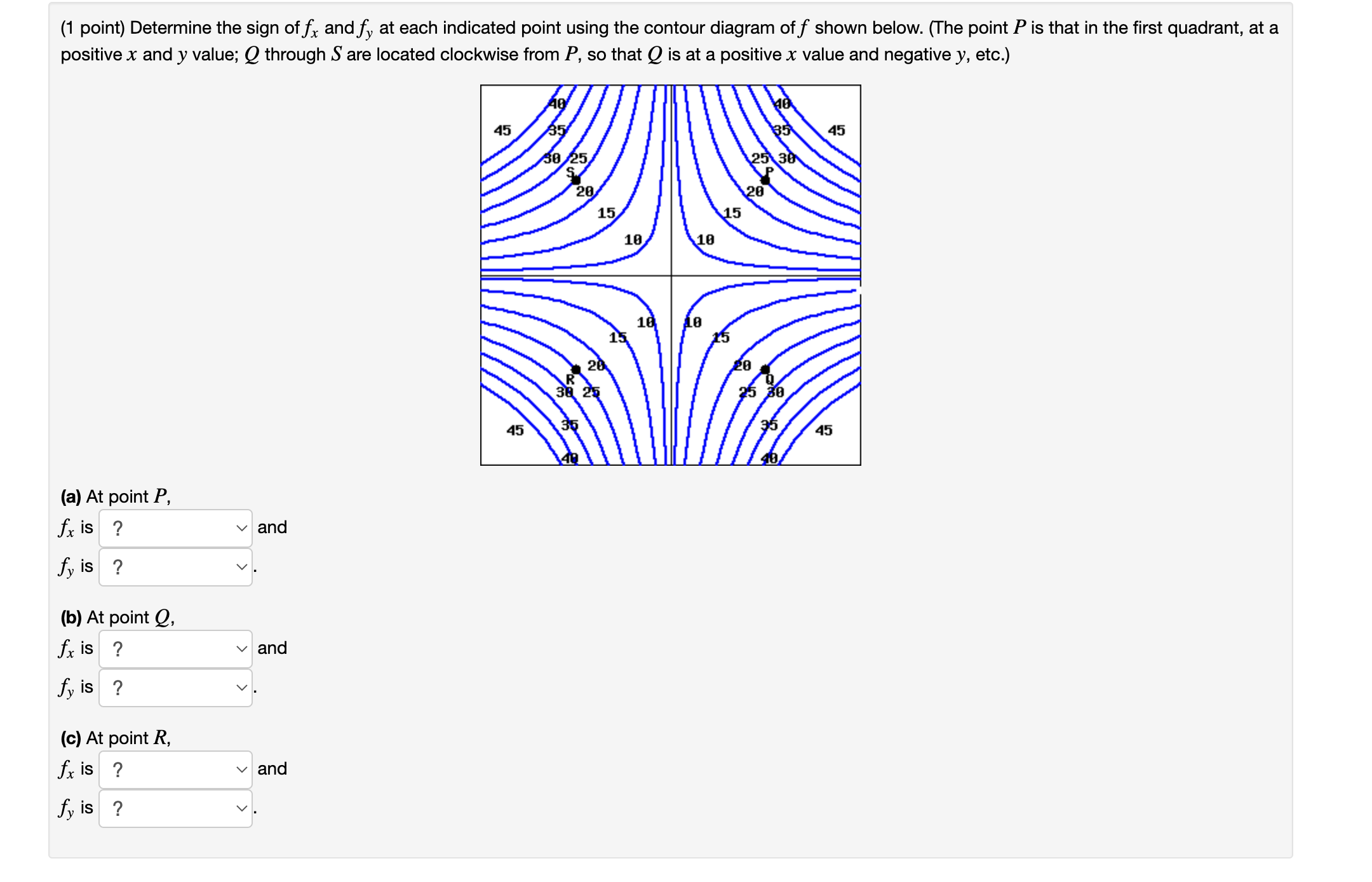
Consider the partial derivatives Is there a function of which has these partial derivatives? Yes If so, what is it? f = (Enter none if there is no such function.) Are there any others? fx(x, y) = 4xy5 - 12xy, fy(x, y) = 5xy4 - 4x. (1 point) Calculate all four second-order partial derivatives and check that fxy = fyx. Assume the variables are restricted to a domain on which the function is defined. f(x, y) = e4xy fxx = fyy fxy = fyx = = | (1 point) Determine the sign of fx and fy at each indicated point using the contour diagram off shown below. (The point P is that in the first quadrant, at a positive x and y value; Q through S are located clockwise from P, so that Q is at a positive x value and negative y, etc.) (a) At point P, fx is ? fy is ? (b) At point Q, fx is ? fy is ? (c) At point R, fx is ? fy is ? and and and 45 45 40 35 30/ 25 20 15 20 38 25 10 10 10 15 10 35 25 30 20 20 25 30 40 45 45 (1 point) The plane y = m = 1 intersects the surface z = x + 5xy y in a certain curve. Find the slope to the tangent line to this curve at the point P = (1, 1, 5). Preview My Answers Submit Answers (1 point) Find the partial derivatives of the function fx(x, y) = fy(x, y) = f(x, y) = [* cc 1 cos(1t + 1t - 5) dt