I would like to get some guidance for these problems as I am very much stuck with them without any progress.

Thank you very much for your help in advance!

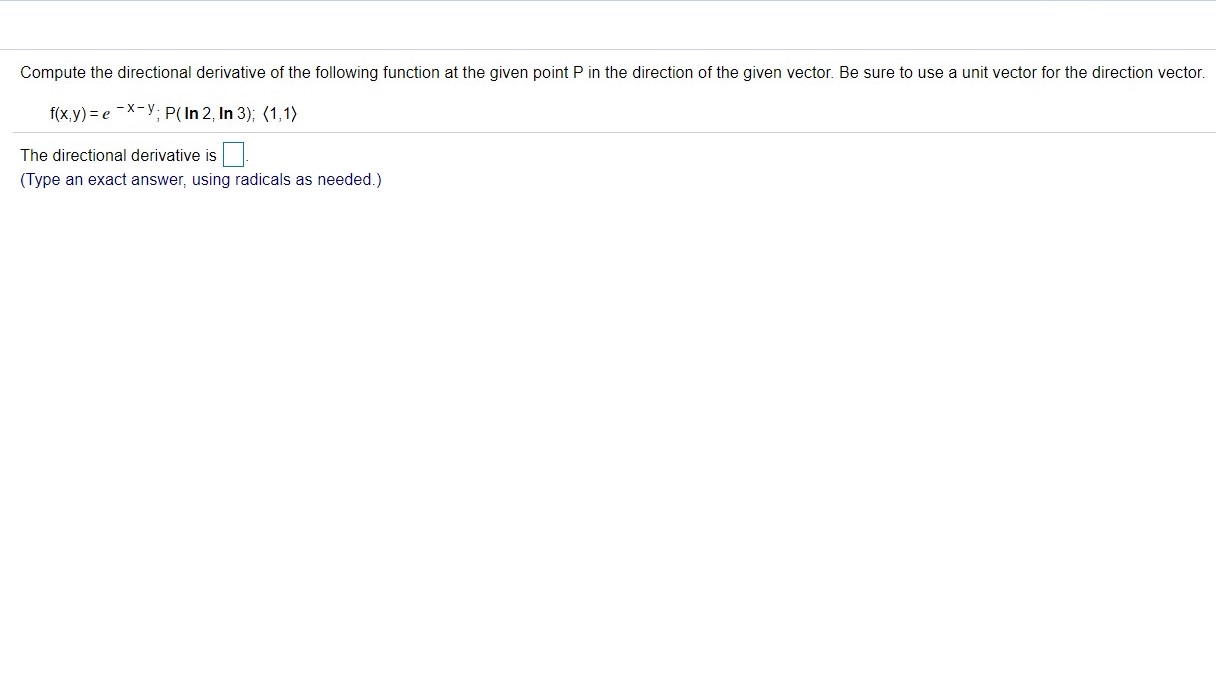
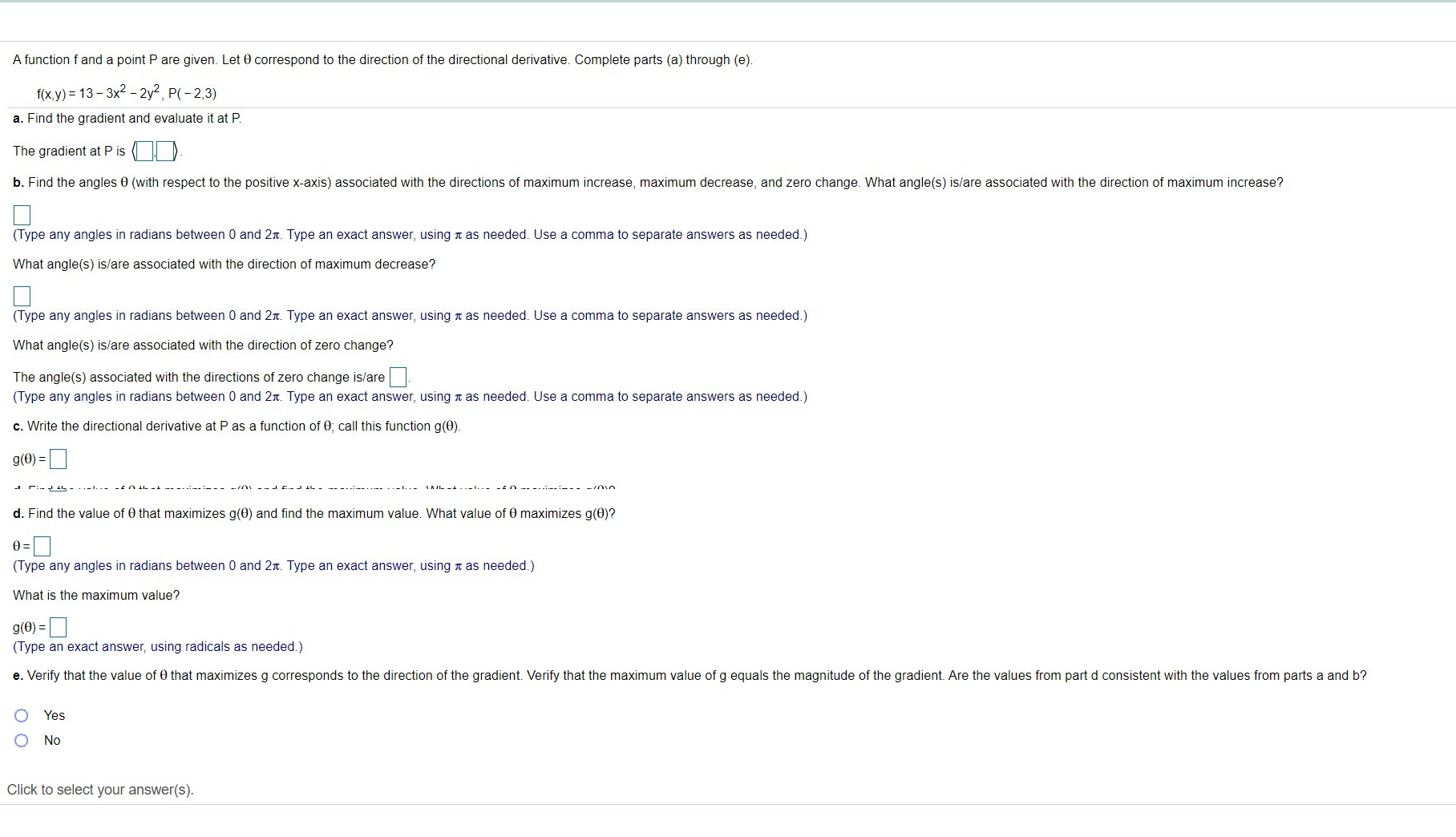
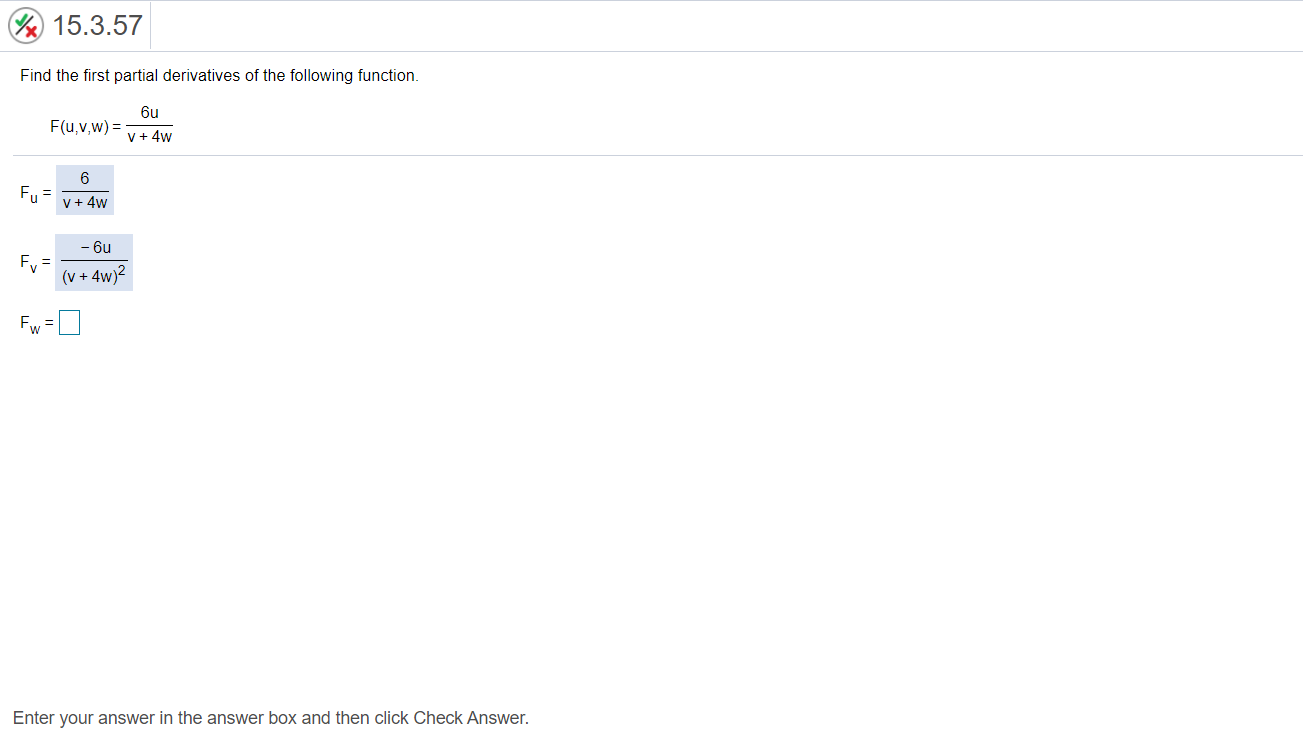
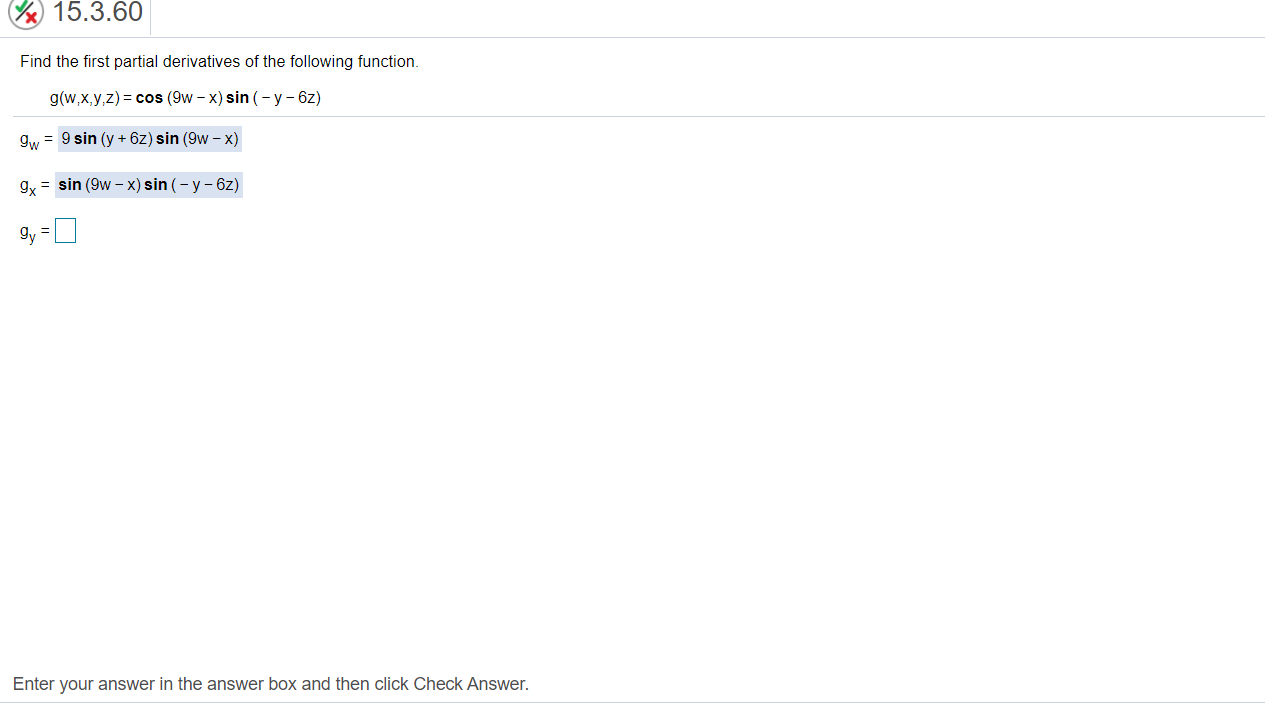
Compute the directional derivative of the following function at the given point P in the direction of the given vector. Be sure to use a unit vector for the direction vector. f(x,y) = e - X-y; P( In 2, In 3); (1, 1) The directional derivative is (Type an exact answer, using radicals as needed.)A function f and a point P are given. Let 0 correspond to the direction of the directional derivative. Complete parts (a) through (e). f(x,y) = 13 - 3x2 - 2y2, P( - 2, 3) a. Find the gradient and evaluate it at P. The gradient at P is ( b. Find the angles 0 (with respect to the positive x-axis) associated with the directions of maximum increase, maximum decrease, and zero change. What angle(s) is/are associated with the direction of maximum increase? (Type any angles in radians between 0 and 2x. Type an exact answer, using it as needed. Use a comma to separate answers as needed.) What angle(s) is/are associated with the direction of maximum decrease? (Type any angles in radians between 0 and 2x. Type an exact answer, using it as needed. Use a comma to separate answers as needed.) What angle(s) is/are associated with the direction of zero change? The angle(s) associated with the directions of zero change is/are. (Type any angles in radians between 0 and 2x. Type an exact answer, using it as needed. Use a comma to separate answers as needed.) c. Write the directional derivative at P as a function of 0; call this function g(0). g(0) = FE- 1 4 - . d. Find the value of 0 that maximizes g(0) and find the maximum value. What value of 0 maximizes g(0)? (Type any angles in radians between 0 and 2xt. Type an exact answer, using x as needed.) What is the maximum value? 9(0) = (Type an exact answer, using radicals as needed.) e. Verify that the value of 0 that maximizes g corresponds to the direction of the gradient. Verify that the maximum value of g equals the magnitude of the gradient. Are the values from part d consistent with the values from parts a and b? O Yes O No Click to select your answer(s).15.3.57 Find the first partial derivatives of the following function. Su F(u, V,W) = V + 4w 6 V + 4w - 6u (v + 4w)2 FW =] Enter your answer in the answer box and then click Check Answer.x 15.3.60 Find the first partial derivatives of the following function. g(w,x,y,z) = cos (9w - x) sin ( - y - 6z) 9w = 9 sin (y + 6z) sin (9w - x) 9x = sin (9w - x) sin ( - y - 6z) gv = Enter your answer in the answer box and then click Check