Consider the second order constant coefficient linear differential equation with initial values y^'' ? 3y^' + 2y = e^3t , y(0) = 0, y^' (0) = 3 .

(a) Find the characteristic polynomial q(s), then find the set B_q.

(b) The B_q in Part (1) should contain two functions. Denote these two functions by y₁ and y₂. Use variation of parameters to find a particular solution y_p toy^'' ? 3y^' + 2y = e^3t .

(c) Now the solution to the initial value problem is of the form y_p + c₁y₁ + c₂y₂ for some undetermined constants c₁, c₂ ? R. Use the initial values to determine c₁ and c₂.

(d) From another point of view, y satisfies a system of first order linear differential equations. (question continues in picture)

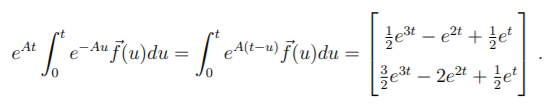
y1 equations. More precisely, let y1 = y, y2 = y' and y = (starting from this part, y2 y1 and y2 have different meaning from Part (a), (b) and (c)). Then we have y1 = y2 0 y(0) = yo = (1) 32 = -291 + 3y2 + eat 3 write the above system in the vector form y' = Ay + f by finding A and f.\f