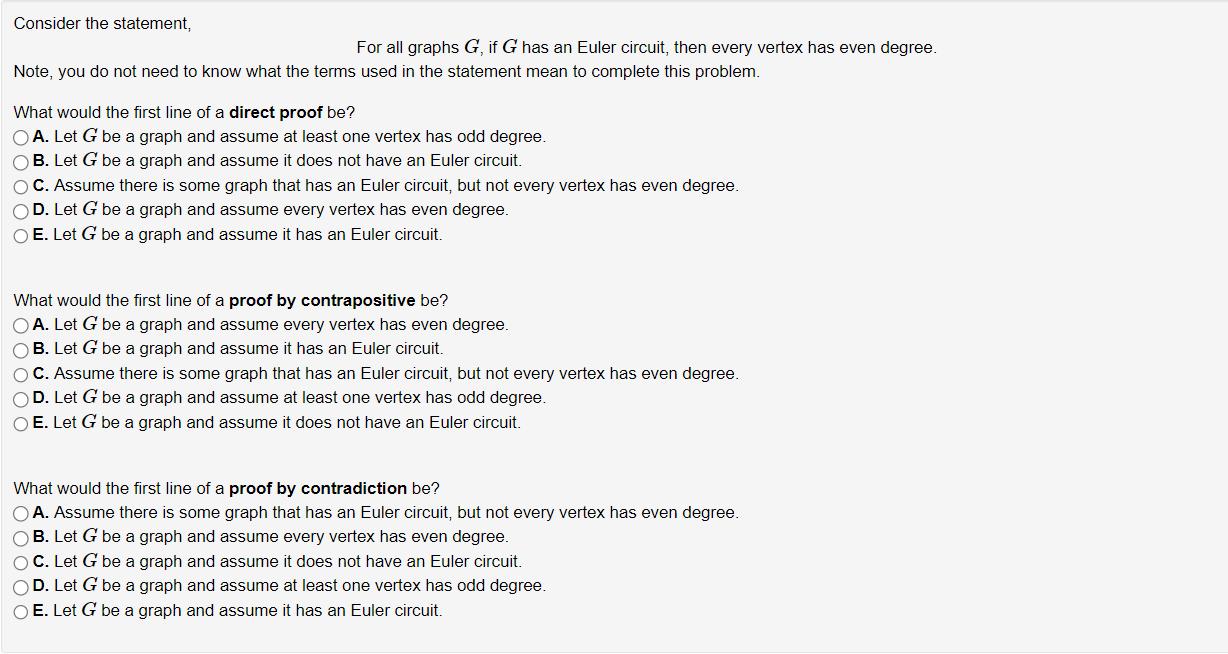
Consider the statement, For all graphs G, if G has an Euler circuit, then every vertex has even degree. Note, you do not need to know what the terms used in the statement mean to complete this problem. What would the first line of a direct proof be? OA. Let G be a graph and assume at least one vertex has odd degree. OB. Let G be a graph and assume it does not have an Euler circuit. OC. Assume there is some graph that has an Euler circuit, but not every vertex has even degree. OD. Let G be a graph and assume every vertex has even degree. O E. Let G be a graph and assume it has an Euler circuit. What would the first line of a proof by contrapositive be? OA. Let G be a graph and assume every vertex has even degree. OB. Let G be a graph and assume it has an Euler circuit. OC. Assume there is some graph that has an Euler circuit, but not every vertex has even degree. OD. Let G be a graph and assume at least one vertex has odd degree. O E. Let G be a graph and assume it does not have an Euler circuit. What would the first line of a proof by contradiction be? OA. Assume there is some graph that has an Euler circuit, but not every vertex has even degree. OB. Let G be a graph and assume every vertex has even degree. OC. Let G be a graph and assume it does not have an Euler circuit. OD. Let G be a graph and assume at least one vertex has odd degree. O E. Let G be a graph and assume it has an Euler circuit.