Consider the vector yi = (yi1, . . . , yip) 0 , whose sample mean is y = 0, and sample variance-covariance matrix is S. Denote the first principal component of y as ?ci = w? 0yi with corresponding eigenvalue ? >? 0. Denote the second principal component as bci = wb 0yi with corresponding eigenvalue ? >b 0. Use this information to answer the following questions:

c) Show that when ?? 6= ?b then the covariance between ?c and bc is zero.

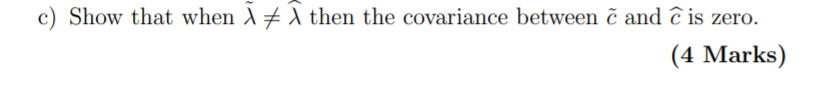
\fConsider the vector yi = (yil, . .., yip) , whose sample mean is y = 0, and sample variance-covariance matrix is S. Denote the first principal component of y as ci = w'y; with corresponding eigenvalue > > 0. Denote the second principal component as ci = wy; with corresponding eigenvalue A > 0. Use this information to answer the following questions