Consider this example:

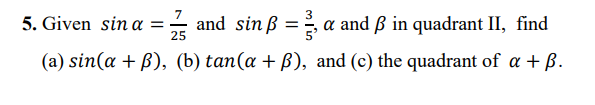
5. Given cosa = - - and cos B = -, a and B in quadrant III, find (a) sin(a + B), (b) tan(a + B), and (c) the quadrant of a + B. 17 15 5 4 B' 8 3 sina = - 13 sinB = 17 8 COSA= cosB = 17 tana = 15 tans = W /A CO (a) sin(A + B) = sinAcosB + cosAsinB = (-9) (9) + (-#) (-3)= 45 + 32 = 77 85 85 85 tanA+tanB 24 45+32 77 77 (b) tan(A + B) = = = 60 - 1-tanAtanB -36 36 24 24 24-60 15 15.348 OR 8 3 38 = = = 17 X 24 77 1 - 15 4 1- 24 36 36 3 24 S A X X X (c ) Quadrant II T X C5. Given sina = and sin B , a and B in quadrant II, find 25 (a) sin(a + B), (b) tan(a + B), and (c) the quadrant of a + B