Consider two independent random samples. The first one Y1,1, , Y1,9 is a random sample from N(1, 2 ) and the second one Y2,1, , Y2,9 is a random sample from N(2, 2 ). The parameters 1, 2, 2 are unknown. We want to conduct hypothesis tesing H0 : 1 = 2 v.s. H1 : 1 6= 2 If we use the two-sample t-test, we would calculate the following test statistic T = Y 1 Y q 2 s 2 p ( 1 9 + 1 9 )

where Y i = PJ j=1 Yij , i = 1, 2 and s 2 p = P2 i=1 P9 j=1(YijYi) 2 9+92 . If we use the F-test from one-way ANOVA, we would calculate the following test statistic F = SSB/(2 1) SSW/(2 (9 1)) where SSB = 9P2 i=1(Y i Y ) 2 and SSW = P2 i=1 P9 j=1(Yij Y i) 2 . Show that F = T 2 . (Hint: show that Y 1 Y = 1 2 (Y 1 Y 2) and Y 2 Y = 1 2 (Y 1 Y 2))

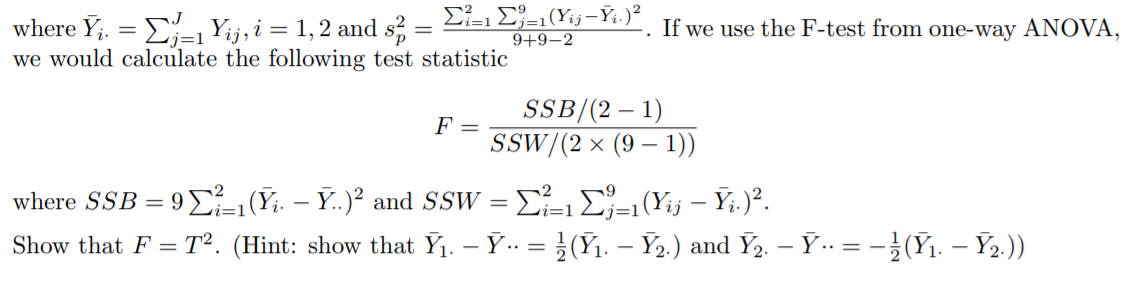
Consider two independent random samples . The first one / 1. 1 . ... . I 1 , is a random sample from N ( H1, 0= ) and the second one 12.1 . .... I2. , is a random sample from N ( 1.2 , 0= ) . The parameters HI. H.2 , O' are unknown . We want to conduct hypothesis tesing* HO : HI = H2 V. S. HI : HI * H.2 If we use the two- sample t-test , we would calculate the following test statistic I' = * 1 . - V/ 2 . ( F + { )Es /where V . = >_, Yiji = 1 . 2 and s ? _ Li= 1 Zilli;- ). If we use the F - test from one - way ANOVA . we would calculate the following test statistic 9 + 9 - 21 F = S' SB / ( 2 - 1 ) S SW / ( 2 X ( 9 - 1 ) ) where S' SB = 9 >_ ( Vi. _ Y. . ) ? and S SW = > > >; - 1 ( Vij - Vi. ) 2. Show that F = I'2. ( Hint : show that / 1. _ Y .. = $ ( Y 1. _ Yz. ) and $2. _ Y .. _ _ = ( Y 1. _ Y 2. ) )