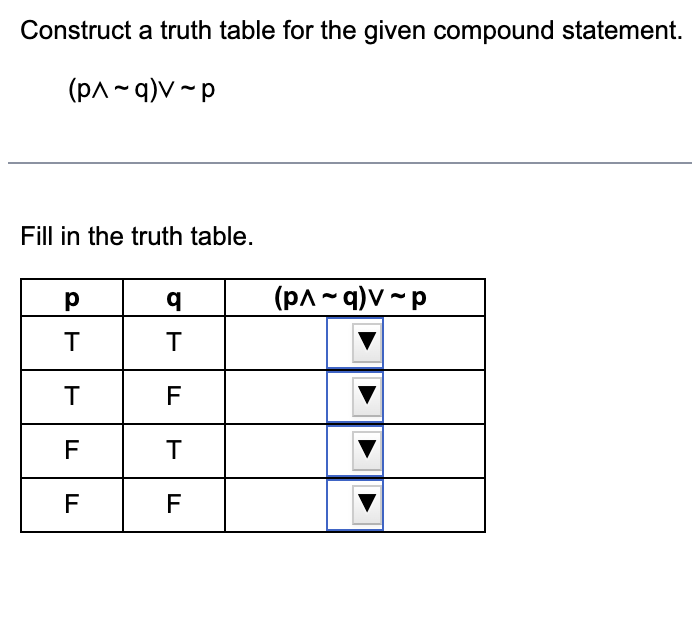
Question: Construct a truth table for the given compound statement. (p^~q)V~p Fill in the truth table. PT q T (p^~q)V~p T T F F T




Construct a truth table for the given compound statement. (p^~q)V~p Fill in the truth table. PT q T (p^~q)V~p T T F F T F F Construct a truth table for the given compound statement. (~qvr)^p Fill in the truth table. PT q r (~qvr)p T T T T T F T F T T TI F F F T T F T F F F T F F F Use De Morgan's laws to write the negation of the following statement. He is not the Cowardly Lion, or he does not want courage. He is the Cowardly Lion, and he wants courage. He is not the Cowardly Lion, or he wants courage. If he is the Cowardly Lion, then he wants courage. He is the Cowardly Lion, or he wants courage. Let s represent "she sings for a living," let t represent "he fixes cars," and let r represent "they collect art." Express the compound statement in words. -st What are the words that express the conditional statement? A. If she does not sing for a living, then he fixes cars. B. If she does not sing for a living, then he does not fix cars. C. If he fixes cars, then she does not sing for a living. D. If she sings for a living, then he fixes cars. Let q represent "I study," let r represent "The chair is broken," and let p represent "I get an A." Write the following compound statement in symbols. I get an A, and if the chair is broken, then I do not study. Choose the correct symbolic form below. OA. (pr)^-q . ( ~q) OC. p (r^ q) OD. p^(r q)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


