Continuing from the previous problem, suppose later in the day the customer arrival rate (customers per hour) will be five times as many per hour vs. the original problem. We respond by using five servers instead of just one. Answer the following for this busier time period:

What is the average server utilization ?

What is the average number of customers waiting in line?

What is the average number of customers in the system? (Waiting in line + being served)

What is the average time (in minutes) spent waiting in line?

What is the average time (in minutes) spent in the system (Waiting in line + being served)

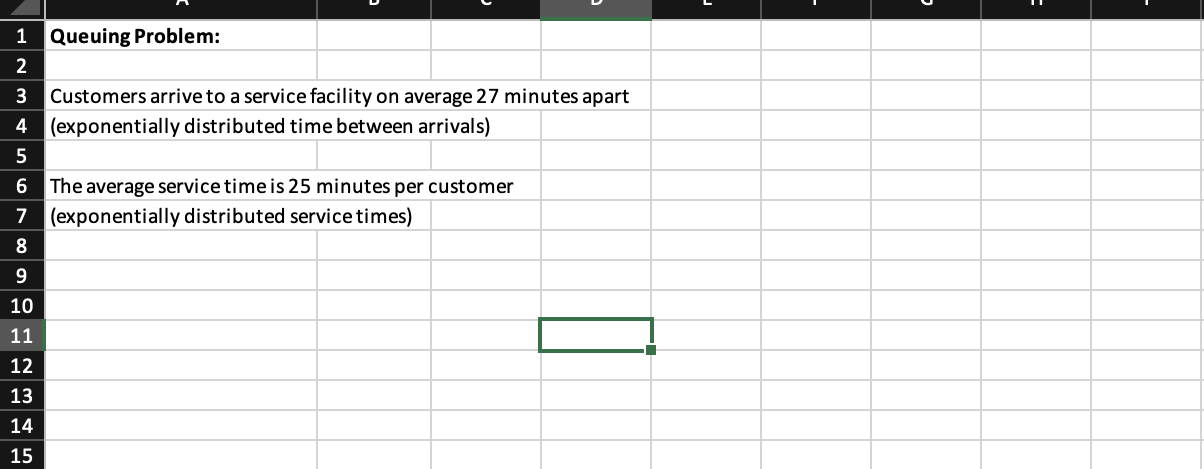
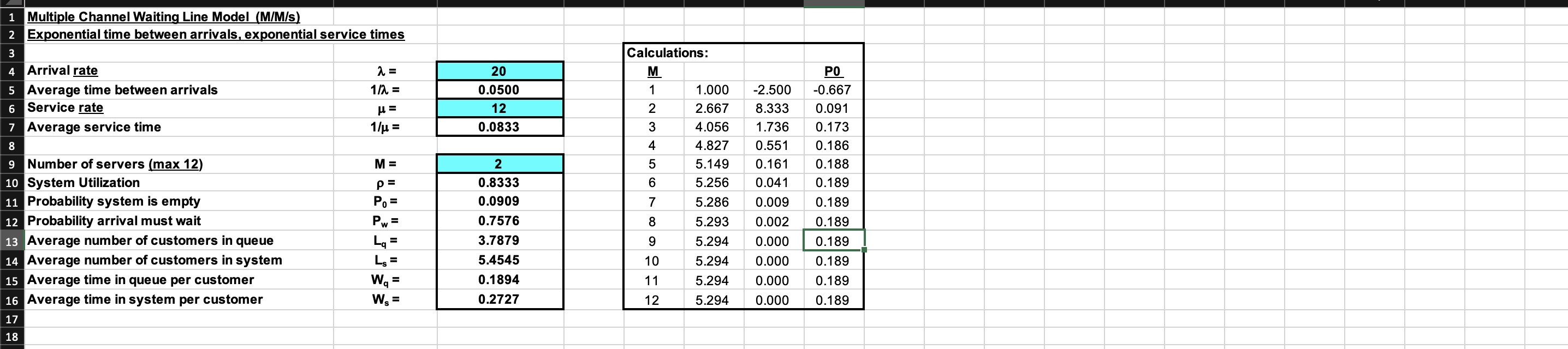
1 Queuing Problem: 2 3 Customers arrive to a service facility on average 27 minutes apart 4 (exponentially distributed time between arrivals) 5 6 The average service time is 25 minutes per customer 7 (exponentially distributed service times) 8 9 10 11 12 13 14 15 20 0.0500 12 0.0833 H= 1 Multiple Channel Waiting Line Model (M/M/s) 2 Exponential time between arrivals, exponential service times 3 4 Arrival rate 2 = 5 Average time between arrivals 1/2 = 6 Service rate 7 Average service time 1/u = 8 9 Number of servers (max 12) M= 10 System Utilization p= 11 Probability system is empty Po= 12 Probability arrival must wait Pw= 13 Average number of customers in queue 14 Average number of customers in system Ls = 15 Average time in queue per customer 16 Average time in system per customer 17 Calculations: M 1 1.000 2 2.667 3 4.056 4 4.827 5 5.149 6 5.256 7 5.286 5.293 5.294 10 5.294 5.294 5.294 -2.500 8.333 1.736 0.551 0.161 0.041 0.009 0.002 2 0.8333 0.0909 0.7576 3.7879 5.4545 0.1894 0.2727 PO -0.667 0.091 0.173 0.186 0.188 0.189 0.189 0.189 0.189 0.189 0.189 0.189 8 9 0 1 2 0.000 0.000 0.000 We = Ws = 0.000 18