Question: Convert the coordinates of the following equations a) Cartesian function (x2 + y2) = yx to polar coordinates. b) Polar function r = sec(0) to


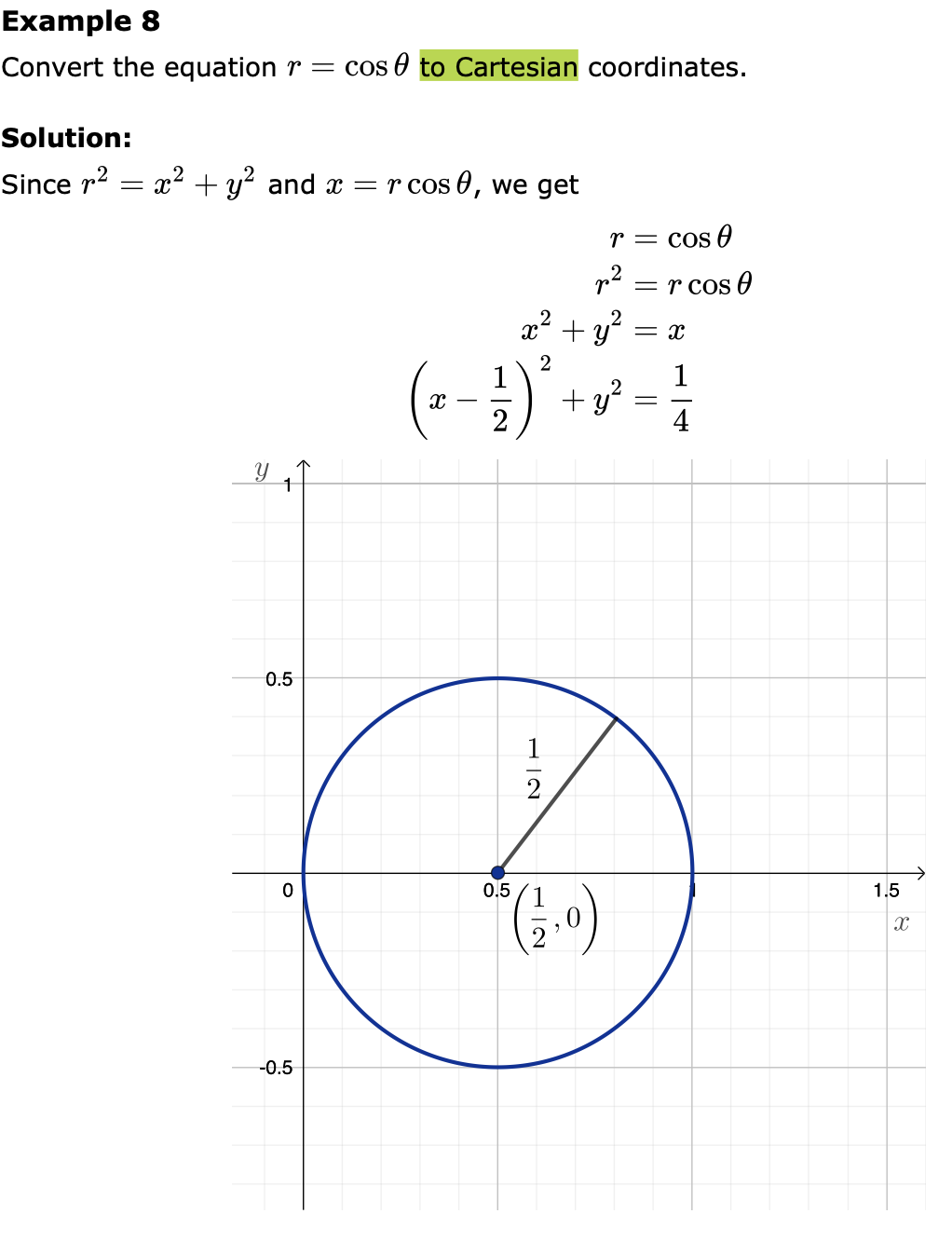
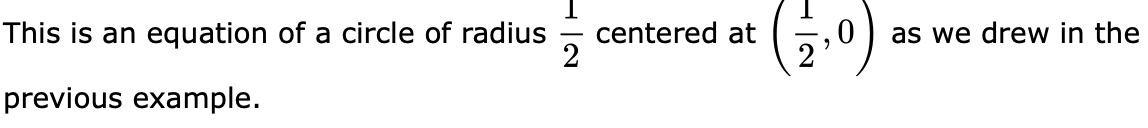
![y2 )3/2 = 203;] to polar coordinates. Solution: Since a: = rcos6](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667ea02d3440a_572667ea02d01566.jpg)
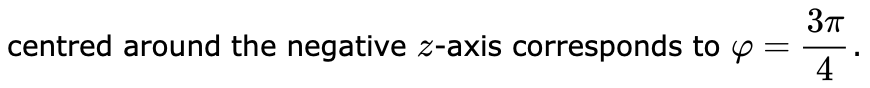
Convert the coordinates of the following equations a) Cartesian function (x2 + y2) = yx to polar coordinates. b) Polar function r = sec(0) to Cartesian coordinates. c) Cylindrical function r + z = 9 to spherical coordinates.'Example 9 Convert the equation of the curve (3:2 -l- y2 )3/2 = 203;] to polar coordinates. Solution: Since a: = rcos6 and y = rsin6 we get (332 +y2)3/2 : 2332/ r3 : 2(r cos 6)(r sin 6) r3 : 1'2 sin 26 7 : sin 26 Notice that the last simplification is only valid since the pole, r = 0, is still included in the graph (the case where 6 = 7r). Observe that since we have the restriction r 2 0 we must also have sin 26 Z 0. Hence, we find that a domain of the function is 0503;, 7r
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


