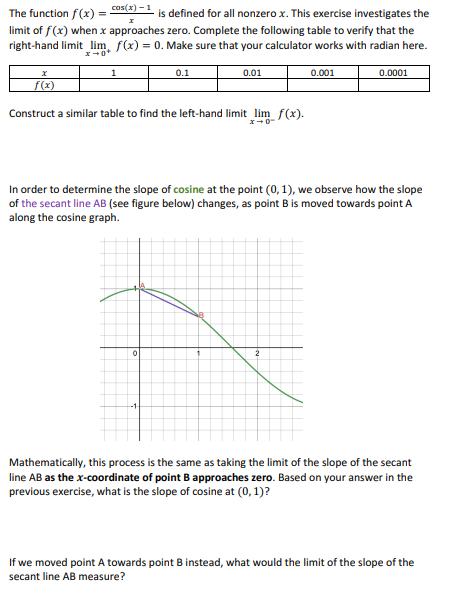
cos(x) - 1 The function f(x) is defined for all nonzero x. This exercise investigates the limit of f(x) when x approaches zero. Complete the following table to verify that the right-hand limit_lim f(x) = 0. Make sure that your calculator works with radian here. 0.001 f(x) = 0.1 0.01 Construct a similar table to find the left-hand limit lim_ f(x). 0 In order to determine the slope of cosine at the point (0, 1), we observe how the slope of the secant line AB (see figure below) changes, as point B is moved towards point A along the cosine graph. 0.0001 2 Mathematically, this process is the same as taking the limit of the slope of the secant line AB as the x-coordinate of point B approaches zero. Based on your answer in the previous exercise, what is the slope of cosine at (0, 1)? If we moved point A towards point B instead, what would the limit of the slope of the secant line AB measure?