Could I please have the solution to the following question:

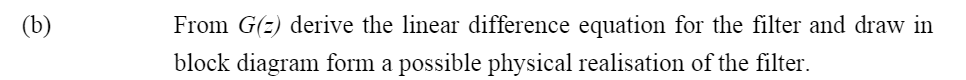
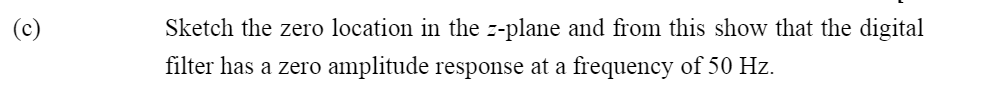
Using the bilinear transform method determine the pulse transfer function, G(z), of a digital notch filter, i.e. a narrow band reject filter, starting from an analogue filter described by the transfer function: G(s)=s2+4s+1s2+1 The filter should have a zero amplitude response at a frequency of 50Hz and a sampling period, T=1/200 seconds, i.e. a sampling frequency, fs= 200Hz. In the normalised form shown above G(s) has a zero amplitude response at 0=1 rad/sec but this can be de-normalised to locate the zero response at a frequency a by applying the transformation sas to the transfer function. The analogue and digital filter frequencies are related by: a=T2tan[2dT]. (Hint: Remember to pre-warp the analogue filter frequency response using this expression to get it to match the required digital filter frequency response at 50 Hz) The bilinear transformation is given by: sT2[z+1z1] From G(z) derive the linear difference equation for the filter and draw in block diagram form a possible physical realisation of the filter. Sketch the zero location in the z-plane and from this show that the digital filter has a zero amplitude response at a frequency of 50Hz