Could someone please check my work

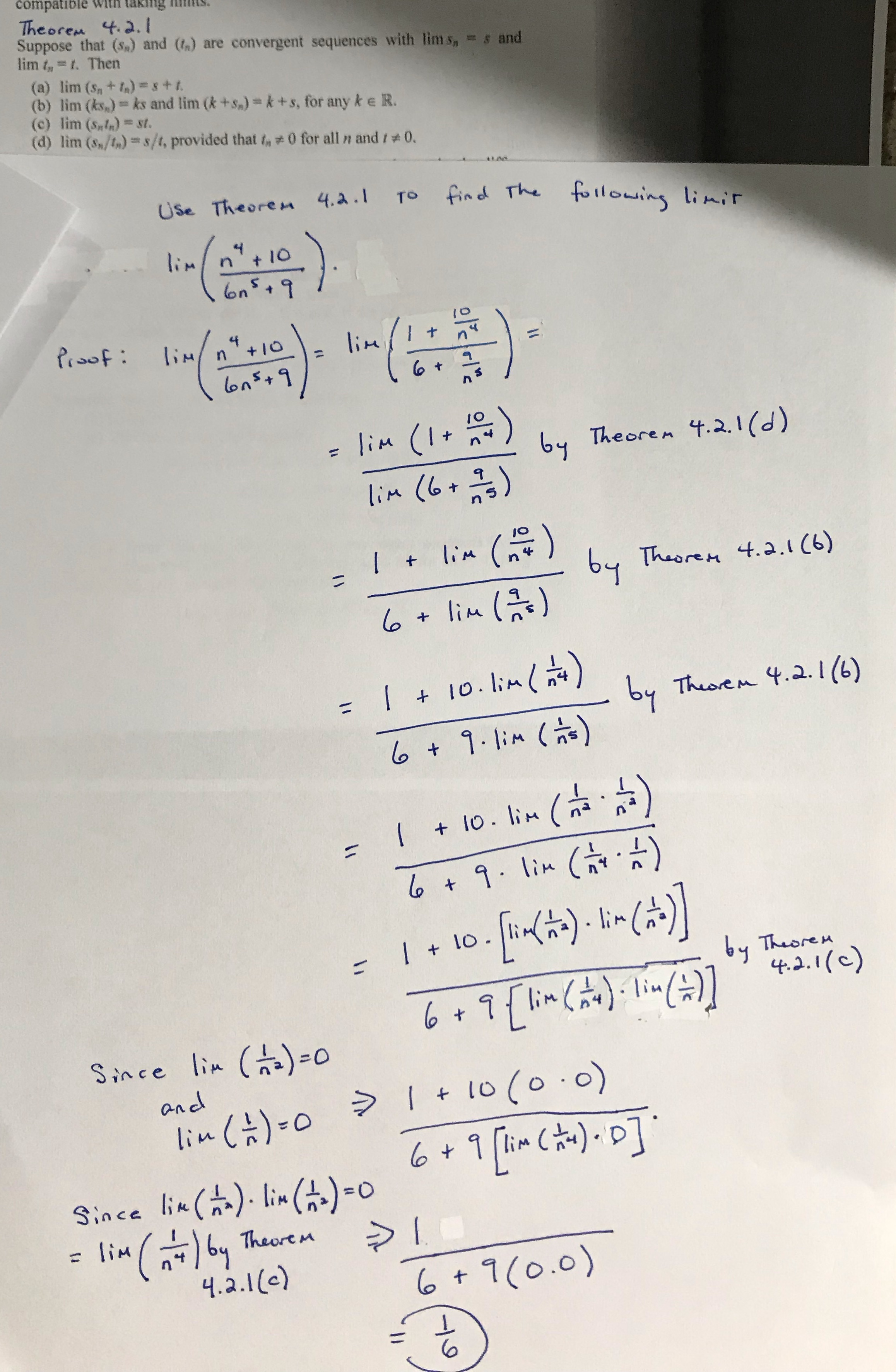
comp Theorem 4.2.1 lim ty = t. Then Suppose that (s,) and (1.) are convergent sequences with lims, = s and (a) lim (S, + 1) = 8+ 1. (b) lim (ks.) = ks and lim (* +s,) = k +s, for any ke R. (c) lim (S,in) = st. (d) lim (s,/t,) = s/t, provided that to * 0 for all n and : # 0. Use Theorem 4.2. 1 To find The following limit lim n + 10 6n5 + 9 Proof: lim / n*+ 10 = lim I + 6on5 + 9 6 2 n s = lim ( 1+ 24 by Theorem 4.2.1 ( d) lim ( 6 + 2 ) = 1+ lim (n4) by Theorem 4.2.1 ( 6 ) 6 + lim (= =) = 1 + 10. lim (14) by Theorem 4.2.1 ( 6 ) 6 + 9. lim ( is) = 1 + 10. lim (me . me) 6 + 9. lim ( 24 . = ) = 1 + 10. ( lim(na) - lim (no) ) by Theorem Since lim (2) = 0 6 + 9 { lim ( 14 ) . lim (= ) ] 4.2. 1 ( c ) and lim ( 1 ) = 0 7 1 + 10 (0 . 0) Since lim ( no ) . lim ( 12 ) =0 6 + 9 lim (Am ) . D] = lim ( -4 ) by Theorem 4.2.1 (c ) 6 + 9 (0.0 )